Как заключить договор с банком. Банковский договор
Научной базой применения концептуальных, конструкторских, технологических и материаловедческих решений для всех этапов создания машин и конструкций должны стать принципы и методы физического и математического моделирования.
Физическое и математическое моделирование в машиностроении базируется на общих подходах, развиваемых на основе фундаментальных наук, прежде всего математики, физики, химии и др. Математическое моделирование и вычислительный эксперимент становятся новым методом анализа сложных машин, рабочих процессов и системы машина - человек - среда. Физическое и математическое моделирование проводится в несколько стадий.
Начинается моделирование с постановки и уточнения задачи, рассмотрения физических аспектов, определения степени влияния на моделируемые процессы различных факторов в программируемых условиях функционирования моделируемых систем или процесса. На этой основе строится физическая модель. Затем на ее базе строится математическая модель, включающая в себя математическое описание моделируемого процесса или механической системы в соответствии с закономерностями кинематики и динамики, поведения материалов под действием нагрузок и температур и т. д. Модель исследуется по таким направлениям, как соответствие поставленной задаче, существование решения и т. п.
На следующей стадии выбирается вычислительный алгоритм решения задачи моделирования. Современные численные методы позволяют снять ограничения на степень сложности математических моделей.
Далее осуществляется программирование
вычислительного алгоритма для ЭВМ
. При этом создаются проблемно-ориентированные пакеты прикладных программ, позволяющие на их основе создавать сложные программы для комплексного описания процессов, машин и систем машин.
На следующей стадии выполняются расчеты на ЭВМ
по разработанным программам. Существенное значение при этом имеет рациональное представление конечных результатов. Завершающая стадия предусматривает анализ полученных результатов, сопоставление их с данными физических экспериментов на натурных образцах изделий. В случае необходимости ставится задача уточнения выбранной математической модели с последующим повторением указанных выше стадий.
После завершения работ по физическому и математическому моделированию формируются общее заключение и выводы по конструкторским, технологическим и эксплуатационным мероприятиям, связанным с созданием новых материалов и технологий, обеспечением условий надежной и безопасной работы машин, удовлетворением требований эргономики и экологии. Создание новых машин и конструкций с повышенным уровнем рабочих параметров, экологических и эргономических требований представляет собой сложную комплексную проблему, эффективное решение которой базируется на физическом и математическом моделировании. Общая схема использования моделирования на различных этапах создания машин представлена на картинке ниже.
Разработка эскизного проекта предусматривает построение физических моделей на основании опыта создания прототипов. Математические модели включают новые знания об анализе и синтезе структурных и кинематических схем, о динамических характеристиках взаимодействия между основными элементами с учетом рабочих сред и процессов. На этом же этапе формируются и решаются в общем виде вопросы экологии и эргономики.
При разработке технического проекта
должен осуществляться переход к физическим моделям основных узлов, испытываемым в лабораторных условиях. К математическому обеспечению технического проекта относятся системы автоматизированного проектирования.
Создание принципиально новых машин (машин будущего)
требует совершенствования методов математического моделирования и построения новых моделей. Это в значительной мере относится к уникальным объектам новой техники (атомная и термоядерная энергетика, ракетная, авиационная и криогенная техника)
, а также к новым технологическим, транспортным аппаратам и устройствам (лазерные и импульсные технологические установки, системы на магнитной подвеске, глубоководные аппараты, адиабатные двигатели внутреннего сгорания и др.)
. При этом для реализации задач математического моделирования необходимы сверхмощные ЭВМ
и дорогостоящие программы.
На этапе рабочего проектирования физическое моделирование предполагает создание макетов и испытательных стендов для проверки конструкторских решений. Математическая сторона этого этапа связана с разработкой автоматизированных систем подготовки технической документации. Математические модели уточняют по мере детализации и уточнения граничных условий задач конструирования.

Одновременно с проектированием решаются конструкторско-технологические задачи выбора материалов, назначения технологий изготовления и контроля. В области конструкционного материаловедения используют экспериментальное определение физико-механических свойств на лабораторных образцах как при стандартных испытаниях, так и при испытаниях в условиях, имитирующих эксплуатационные. При изготовлении высокоответственных деталей и узлов из новых материалов (высокопрочные коррозионно- и радиационно стойкие, плакированные, композиционные и др.) необходимо проводить специализированные испытания по определению предельных состояний и критериев повреждения. Математическое моделирование используют для построения имитационных моделей механического поведения материалов в различных условиях нагружения с учетом технологии получения материалов и формообразования деталей машин. Имитационные модели используют при выполнении сложного математического анализа тепловых, диффузионных, электромагнитных и других явлений, сопутствующих новым технологиям.
На основе физических и имитационных моделей
получают сложный комплекс физико-механических свойств, характеристики которых должны использоваться при создании на базе ЭВМ
банков данных о современных и перспективных материалах.
На этапе разработки технологии изготовления деталей, узлов и машин в целом физическое моделирование используют при лабораторной и опытно-промышленной отработке технологических процессов как традиционных (механообработка, литье и др.)
, так и новых (лазерная обработка, плазменная, взрывная, магнитно-импульсная и др.)
.
Параллельно с технологическими процессами разрабатываются физические модели, а также принципы контроля и дефектоскопии материалов и готовых изделий. Математические модели технологических процессов позволяют решать сложные задачи теплопроводности, термоупругости, сверхпластичности, волновых и других явлений с целью рационального выбора для данных деталей эффективных методов и параметров обработки.
На этапе создания машин и конструкций , когда осуществляется доводка и испытания головных образцов и опытных партий, физическое моделирование предусматривает проведение стендовых и натурных испытаний. Стендовые испытания обеспечивают высокую информативность и сокращают сроки доводки опытных образцов изделий массового и крупносерийного производства. Натурные испытания* необходимы для оценки работоспособности и надежности уникальных изделий на предельных режимах. При этом задачами математического моделирования становятся алгоритмы и программы управления испытаниями. Анализ получаемой экспериментальной информации следует проводить на ЭВМ в реальном масштабе времени.
При эксплуатации машин физическое моделирование используют для диагностики состояния и обоснования продления ресурса безопасной работы. Математическое моделирование на этом этапе имеет- целью построение моделей эксплуатационных повреждений по комплексу принятых при проектировании критериев: Проработка таких моделей выполняется в настоящее время для объектов атомного и теплового энергетического машиностроения, ракетной и авиационной техники и других объектов.
Математическое моделирование позволяет автоматизировать управление рабочими режимами с помощью ЭВМ по заданным программам, обеспечить оптимальное регулирование переходных процессов и исключить с помощью автоматизированных систем защиты достижение предельных ситуаций, ведущих к аварийным отказам.
В области естественных наук наиболее распространенными являются два вида моделирования - физическое и математическое .
Процесс физического моделирования состоит в изучении системы посредством анализа некоторого макета, сохраняющего физическую природу системы или внешне напоминающего изучаемый объект.
Физические модели (их еще называют натурными) могут иметь вид полномасштабных макетов (например, тренажеры летательных аппаратов), могут выполняться в уменьшенном масштабе (глобус) или в увеличенном масштабе (планетарная модель атома). В инженерной практике широко используются как макеты в натуральную величину, так и уменьшенные модели объектов. В последнем случае параметры экспериментов с физической моделью выбираются из подобия.
Примерами физических моделей являются: модели летательного аппарата или автомобиля, исследуемые в аэродинамической трубе; построенный на базе военного истребителя миниатюрный аналог сверхзвукового пассажирского лайнера, используемый во время летных испытаний.
Статические физические модели, такие как макеты архитектурных объектов или заводских корпусов, позволяют наглядно представить пространственные соотношения.
Однако модели физического типа имеют ограниченную сферу применения. Не для всяких явлений и объектов могут быть построены дающие значимые результаты физические аналоги.
Математическая (или символическая) модель концентрирует в себе записанную в форме математических соотношений совокупность наших знаний, представлений и гипотез о соответствующем объекте или явлении.
Математическая модель - абстрактный образ системы, отражающий ее важнейшие свойства. Поскольку математические модели являются абстрактными и, следовательно, наиболее общими, то именно они находят самое широкое применение в исследовании систем.
Натурные эксперименты представляют собой источник информации ограниченного объема. Математическая модель допускает более широкие исследования и обобщения, результаты которых дают информацию для прогнозирования поведения системы в будущем. Правда, чтобы обеспечить эти возможности, приходится решать проблему соответствия (адекватности ) модели и системы, т.е. проводить дополнительное исследование согласованности результатов моделирования с реальной ситуацией.
Математические модели строят на основе законов и закономерностей, выявленных фундаментальными науками: физикой, химией, экономикой, биологией и т.д. После того как модель сформулирована, необходимо исследовать ее поведение. С усложнением анализируемых объектов использование для этих целей аналитических методов возможно лишь в ограниченном количестве случаев. Выход состоит в переходе к машинным реализациям математических моделей.
Математические машинные модели делят на аналоговые и цифровые в соответствии с типами вычислительных машин, на которых они реализованы.
Аналоговое моделирование основано на том факте, что различные по природе явления и процессы могут иметь одинаковое математическое описание. Хорошо известным примером служит описание одними и теми же уравнениями электрического колебательного контура и пружинного маятника. На аналоговых вычислительных машинах эти уравнения воспроизводятся обычно с помощью электрических схем, построенных на электронных операционных усилителях и функциональных блоках, моделирующих предопределенный набор математических действий и функций, например арифметические действия, интегрирование, нелинейные функции. Искомые характеристики исследуемой системы регистрируются путем измерения на модели соответствующих электрических величин. Переработка информации в такой модели носит параллельный характер и реализуется в форме электрического процесса, происходящего в собранной схеме.
Цифровые модели, реализуемые на цифровых электронных вычислительных машинах, представляют собой алгоритмы переработки входной информации в выходную. Входной информацией могут быть параметры модели, ее начальные состояния и т.п., а выходной - траектории этой модели.
Моделирующий алгоритм строится на основе математической модели системы. Последняя может быть как алгоритмической , так и аналитической .
Примером алгоритмической модели является конечный автомат, заданный с помощью одношаговой функции перехода, которая собственно и определяет алгоритм пересчета состояний автомата, т.е. воспроизведения ее траектории.
Примером аналитической модели является система обыкновенных дифференциальных уравнений, в которой для получения решения необходимо использовать какой-либо метод интегрирования. Данная модель преобразуется в алгоритмическую при использовании метода численного интегрирования. Такое преобразование приводит, вообще говоря, к изменению свойств модели, что в принципе должно учитываться при исследовании.
При расчете физических процессов составляется математическая модель - система уравнений, описывающая зависимости между физическими величинами при некоторых упрощающих допущениях. Например, при движении точки вблизи поверхности Земли полагается ускорение свободного падения постоянным, не зависящим от высоты расположения точки над поверхностью. Для тел, движущихся с небольшой скоростью или в разряженной атмосфере, пренебрегают сопротивлением воздуха. Само точка часто заменяют материальной точкой, т. е. размерами точки пренебрегают. Физические процессы описываются, как правило системой дифференциальных уравнений, для решения которой применяют различные численные методы (модели). Широко используется метод конечных разностей, в котором бесконечно малые приращения переменных заменяют малыми (конечными) приращениями.
Например, изменение параметра времени представляют в виде:dt=t 2 -t 1 , а изменение функции "Х": dX(t) = X(t)-X(t-dt) = X(t 2)-X(t 1) = X 2 -X 1 .
Рассмотрим задачу определения траектории точки, движущегося в некоторой плоскости под действием различных сил. Например, необходимо вычислить траекторию движения снаряда с учетом сопротивления воздуха или ракеты с учетом изменения ее массы, движущихся в поле тяготения Земли.
Координаты точки X(t), Y(t) в некоторый момент времени "t" можно определить, зная координаты точки X(t-dt), Y(t-dt) в предыдущий момент времени "t-dt" и изменение (приращение) координат dX, dY:
X(t) = X(t-dt) + dX(t),
Y(t) = Y(t-dt) + dY(t).
Если временной интервал выбрать достаточно малым, то можно полагать, что скорость точки на этом интервале не изменяется и приращения координат определяются по формулам:
dX(t) = Vx(t)dt,
dY(t) = Vy(t)dt.
Здесь Vx(t), Vy(t) - проекции скорости на оси координат.
Составляющие скорости Vx(t) и Vy(t) можно вычислить по формулам:
Vx(t) = Vx(t-dt) + Ax(t)*dt,
Vy(t) = Vy(t-dt) + Ay(t)*dt.
Здесь Ax(t), Ay(t) - проекции ускорения на оси координат.
Ускорение определяется силами, действующими на точка: ускорение равно равнодействующей силе, деленной на массу точки. Силы могут зависеть от координат точки, времени и скорости точки. Например, ускорение ракеты в поле тяготения планеты обратно пропорционально квадрату расстояния до центра планеты. При включении двигателя ракеты ускорение зависит от времени (программы работы двигателя). При движении в плотных слоях атмосферы на ракету действуют силы сопротивления воздуха, зависящие от скорости движения, т. е. ускорение зависит от скорости.
Приведем алгоритм расчета траектории движения точки:
1. Определяем силы, действующие на точка, и находим проекции ускорения на оси координат. В общем случае ускорение точки зависит от многих факторов и в момент времени t задается как функция от времени, скорости и координат точки:
Ax:= Fx(Vx, Vy, X, Y, t); Ay:= Fy(Vx, Vy, X, Y, t);
Где Vx, Vy, Ax, Ay - проекции скорости и ускорения.
2.Задаем начальное положение точки - координаты X, Y и начальную скорость и ускорение в виде проекций на оси координат:
X:= X0; Y:= Y0; Vx:= V*cos(fi); Vy:= V*sin(fi);
Ax:= Fx(Vx, Vy, X, Y, t);
Ay:= Fy(Vx, Vy, X, Y, t);
Где V - начальная скорость точки, fi - угол наклона вектора скорости к оси Х.
3. Задаем временной шаг dt и разбиваем весь временной интервал на N участков. При равномерной разбивке приращение времени определяется по формуле:
dt:= (t[N]-t)/(N-1); Здесь (t[N] - t) - время движения точки.
Выбор величины dt определяется необходимой точностью расчета, возможностями вычислительной техники, и может уточняться при решении задачи.
4.Вычисляем массивы скорости, ускорения и координат точки:
For i:= 2 to N do begin
Vx[i]:= Vx + Ax*dt;
Vy[i]:= Vy + Ay*dt;
X[i]:= X + 0.5*(Vx + Vx[i])*dt;
Y[i]:= Y + 0.5*(Vy + Vy[i])*dt;
Ax[i]:= Fx(Vx[i], Vy[i], X[i], Y[i], t[i]);
Ay[i]:= Fy(Vx[i], Vy[i], X[i], Y[i], t[i]);
{ уточняем скорость точки в расчетной точке }
VX[i]:= VX + 0.5*(Ax + Ax[i])*dt;
VY[i]:= VY + 0.5*(Ay + Ay[i])*dt;
Для уменьшения погрешностей расчетной схемы, скорость и ускорения на участке интерполируются средними значениями.
5. Строим траекторию движения точки . Здесь удобно использовать процедуры из библиотеки построения графиков GR_F. Следует определить расчетную область и область рисования траектории на экране. Траектория на экране рисуется процедурой: PutPixel_G(X[i], Y[i], N);
Для тестирования работы алгоритма рассмотрим задачу расчета траектории точки, движущегося из точки с координатами X, Y с начальной скоростью Vx, Vy под действием сил, вызывающих ускорение точки Ax, Ay. Следуя пунктам 1. . 5 приведенного выше алгоритма необходимо рассчитать траекторию движения точки и сравнить с траекторией точки, описанной аналитической зависимостью X(t), Y(t).
Практическое задание N 2. 22
N X 1 Y 1 Vx 1 Vy 1 Axi Ayi X(t) Y(t)
1 0 0 0 b 2*a -y a*t 2 b*sin(t)
2 0 0 a b 0 -y a*t b*sin(t)
3 1 0 1 1 -2*y 2*x e t * cos(t) e t *sin(t)
4 a 0 0 0 -x x*b/a a* cos(t) b*(1-cos(t))
5 a b 0 0 -4*x y a* cos(2*t) b*cos(t)
6 0 0 0 b 2*a 0 a*t 2 b*t
7 2*a 0 0 a x 0 a*(e t + e -t) a*t
8 0 b a 0 -x -y a* sin(t) b*cos(t)
Y
V
 F, *
V 0
g
fi
0 X F, *
V 0
g
fi
0 X
|
Рассмотрим задачу расчета траектории снаряда, движущегося с начальной скоростью "V 0 " под углом "fi" к горизонту с учетом сил сопротивления воздуха, пропорциональных скорости снаряда. Проекции ускорений определим в виде функций:
FUNCTION Fx(Vx, kc: real): real; begin Fx:= - kc*Vx end;
FUNCTION Fy(Vy, kc: real): real; begin Fy:= - kc*Vy - g end;
Где kc - коэффициент сопротивления воздуха,
g = 9. 81, м/с - ускорение свободного падения у поверхности Земли.
Поскольку время подлета снаряда к цели неизвестно, то параметр "dt" выбирается приближенно, например, исходя из максимального времени полета снаряда над горизонтальной поверхностью без учета сопротивления воздуха: tмах= 2*V*sin(fi)/g. Для N = 500, dt = t/500. При решении конкретных задач процесс расчета прекращается при достижении снарядом цели, либо при ограничениях по статическим координатам, например:
REPEAT i:=i+1;
{операторы расчета массивов скорости, ускорения и координат точки }
Until (cc = GetPixel_G(X[i], Y[i])) or (Y[i] < 0) or (i = N);
Здесь cc - цвет пикселов цели, Y[i] < 0 - ограничение по горизонтальной поверхности, i = N - ограничение по размеру массива. В случае преждевременного завершения полета снаряда необходимо увеличить dt или параметр N.
Практическое задание N 2. 23
1. Рассчитать разностным моделированием и по аналитической зависимости траектории полета снаряда без учета сопротивления воздуха. Построить траектории полета снаряда. Начальная скорость V 0 =1000, м/с, угол fi=450. Аналитическая зависимость имеет вид:
X = V 0 *t*cos(fi); Y = V 0 *t*sin(fi) - g*t 2 /2;
2. Рассчитать разностным моделированием и по аналитической зависимости траектории полета снаряда с учетом сопротивления воздуха, пропорциональным скорости снаряда. Построить траектории полета снаряда. Начальная скорость V 0 =3000, м/с, угол fi = 45 0 . Коэффициент сопротивления воздуха kc = 0. 01,с -1 .
Аналитическая зависимость имеет вид:
X=V 0 *cos(fi)*(1-e (-kc*t))/kc; Y=(V 0 *sin(fi)+g/kc)*(1-e (-kc*t))/kc-g*t/kc;
3. Рассчитать разностным моделированием траектории полета снаряда с учетом сопротивления воздуха, пропорциональным квадрату скорости снаряда. Коэффициент сопротивления воздуха kc 1 = kc 2 . Построить совместно траектории полета снаряда для п. 1, 2, 3. Начальная скорость V 0 = 3000, м/с, угол fi = 45 0 .
4. Составить программу поражения неподвижной цели при kc 1 = kc 2 . Изменяя в цикле угол fi на небольшую величину, определить в программе угол при котором будет поражена цель - небольшой прямоугольник с координатами вершин (x1, y1) и (x2, y2). Построить все траектории полета снаряда.
Примечание к п. 1. . 4: Выводить на экран исходные данные: V 0 , fi, kc, а также наибольшую высоту и дальность полета снаряда.
Рассмотрим задачу расчета траектории космического тела , в поле тяготения планеты без учета сил сопротивления. В начальный момент времени тело движется на высоте "Н" со скоростью "V 0 ", направленной по касательной к окружности радиуса R 0 . Поскольку движение спутника вокруг планеты достаточно продолжительно, то не целесообразно запоминать в оперативной памяти все параметры (координаты, скорости и ускорения) в каждый момент времени. Обычно эти параметры, записываются в файл на диск при вычислениях через некоторые моменты времени, а траекторию строят сразу, либо запуская отдельную программу, считывающую данные из файла. Расчетная область задается исходя из оценочных расчетов. Для спутника, движущегося вокруг Земли, можно принять:
Xmin= Ymin= -Kv*R 0 , Xmax= Ymax= Kv*R 0 ,
Здесь R 0 = (Rz+H), Rz=6. 37*10 6 , м. - радиус Земли.
Kv=1. 5 при V 0 <= W 1 ; Kv=10 при W 1 < V 0 < W 2 ; Kv=20 при V >= V 2 .
W 1 = Rz*Ö(g/R 0) - первая космическая скорость,
W 2 = Ö2* W 1 - вторая космическая скорость.
Параметр "dt" можно определить приближенно по формуле: dt=T/N,
где T= 6. 28*Rz/W 1 - время оборота спутника вокруг Земли, N=300.
Расстояние от спутника до центра планеты определяется через координаты:
function R(x, y: double): double; begin R:= sqrt(x*x + y*y) end;
Проекции ускорений определим в виде функции:
function FA(x,r,kz: double):double; begin FA:= -kz*x/(r*r*r) end;
Здесь kz = 4. E+14 для Земли (в системе СИ).
Пусть в начальный момент времени известны координаты спутника:
x 1 = R 0 ; y 1 = 0; r 1 = R(x 1 , y 1);
скорость: Vx 1 = 0; Vy 1 = V 0 ;
и ускорение: Ax 1 = FA(X 1 , r 1 , kz); Ay 1 = FA(Y 1 , r 1 , kz);
Отметим, что скорость в начальный момент времени направлена по касательной к окружности радиуса r 1 .
Для записи алгоритма расчета траектории необходимо знание параметров в двух соседних точках, например, в точке "1" - для предшествующего момента времени и в точке "2" - для расчетного момента времени. Расчет производим в цикле с одновременным выводом траектории движения спутника на экран до тех пор пока выполняется ограничение по радиусу траектории или не нажата любая клавиша.
While (r1< Xmax) or (r1> Rz) or (not keyPressed) do begin
Vx2:= Vx1 + Ax1*dt; Vy2:= Vy1 + Ay1*dt;
X2:= X1 + 0.5*(Vx1 + Vx2)*dt;
Y2:= Y1 + 0.5*(Vy1 + Vy2)*dt; r2:= R(x2, y2);
Ax2:=FA(X2, r2, kz);
Ay2:=FA(Y2, r2, kz);
Vx2:= Vx1 + 0.5*(Ax1 + Ax2)*dt; { уточняем скорость }
Vy2:= Vy1 + 0.5*(Ay1 + Ay2)*dt;
{ Переопределяем значения параметров в точке }
x1:= x2; y1:= y2; r1:= r2;
Vx1:= Vx2; Vy1:= Vy2; Ax1:= Ax2; Ay1:= Ay2
PutPixel_G(x1,y1,c); { Строим траекторию движения точки, c - цвет точки }
Практическое задание N 2. 24
r = P/(1 + e*cos(fi));
где e = P/R 0 - 1; P = (V 0 * R 0 /Rz) 2 /g ; 0 <= fi = 2*Pi.
В начальный момент времени известны координаты спутника: x 1 = R 0 ; y 1 = 0;
и скорость: Vx 1 = 0; Vy 1 = V 0 ; Рассмотреть случаи:
1_1. Начальная скорость V 0 <= W 1 , высота H = 300000, м.
1_2. Начальная скорость W 1 <= V 0 < W 2 , высота H = 400000, м.
1_2. Начальная скорость V 0 >= W 2 , высота H = 500000, м.
Примечание: Построить траектории полета спутника. Через равные промежутки времени выводить на экран время полета спутника, скорость и высоту.
1) V 0 Rz Rz 2) Rz V 0 Rz
 |
|||
 |
|||
1) 20 *Rz 2) 20 *Rz
Рассмотрим задачу расчета траектории точки переменной массы , движущегося под действием реактивной тяги. Движение точки в этом случае описывается уравнением Мещерского:
A = (U/M)*(dM/dt) + F/M
Где A - ускорение точки, M - масса точки.
U - скорость реактивной струи относительно точки,
F - результирующая внешних сил, действующих на точку,
Учитывая, что F = kz*M/r 2 - сила притяжения направлена к центру Земли, а P = U*(dM/dt) - реактивная сила двигателя (тяга) направлена по касательной к траектории движения, определяем проекции ускорения на оси координат:
Ax = P*Vx/(M*V) - kz*x/(r 3); Ay = P*Vy/(M*V) - kz*y/(r 3);
Где V = Ö(Vx 2 + Vy 2) - скорость точки,
r = Ö(x 2 + y 2) - расстояние до центра Земли,
Vx , Vy - проекции скорости точки на оси координат, x, y - координаты точки.
Полагая расход топливаz = dM/dt постоянным, массу точки можно определить по формуле: M = M 0 - z*t; при t < Tk ,
где M 0 - начальная масса точки, Tk - время работы двигателя.
Практическое задание N 2. 25
1. Построить десять траекторий полета баллистической ракеты, рассчитанных разностным моделированием. Начальная скорость V 0 =1,м/с, тяга двигателя P=2. 5Е6,н, стартовая масса M 0 = 1. 5Е5, кг, расход топлива z= 700, кг/с, время работы двигателя Tk = 200, с.
2. Построить траектории полета двухступенчатой баллистической ракеты, рассчитанные разностным моделированием. Начальная скорость V 0 = 1,м/с, стартовая масса M 0 = 3Е5, кг, для первой ступени: тяга P 1 =5Е6, н, расход топлива z 1 = 1700, кг/с, время работы двигателя Tk 1 = 130, с. Для второй ступени: тяга P 2 = 1. 1Е6, н, расход топлива z 2 = 300, кг/с, время работы двигателя Tk 2 = 230, с.
Примечание к п. 1, 2: сопротивление воздуха и вращение Земли не учитывать. Угол запуска ракеты к горизонту = 90 0 -N*0. 002 0 , где N= 1, 2, 3, ..., 10. Во время работы двигателя dt=0. 05, c, затем dt=0. 5, c.
3. Построить траекторию полета спутника Земли при включении двигателя, рассчитанную разностным моделированием. Начальные условия на высоте H=400000 м принять следующие: скорость V 0 =W 1 и направлена по касательной к окружности, M 0 =11000, кг, тяга двигателя P=4Е5, н, расход топлива z=100, кг/с, время работы двигателя Tk = 70, с. Рассчитать скорость спутника при работе двигателя по формуле Циолковского: V = V 0 + U*ln(M 0 /M) , где U = P/z .
Через каждые 10 секунд выводить на экран время полета спутника и скорость.
Рассмотрим задачу расчета траектории точки, прикрепленной к упругой нити , и движущейся с начальной скоростью "V 1 " под углом "fi" к оси "x" из точки с координатами (x 1 , y 1), без учета сил сопротивления воздуха. Эта задача моделирует известную игрушку - мяч, привязанный на резинке.
Пусть точка имеет массу "M", длина нити "L". Полагаем, что нить невесома и абсолютно упруга. Коэффициент упругости "Kn".
Оси координат проведем через точку закрепления нити вверх и влево. Расчетную область ограничим: X_min = Y_min = -Lm, X_max = Y_max = Lm,
где Lm = abs(V 1 * Ö(M/Kn)) + Ö(x12 + y12) + L + 2*M*g/Kn.
| Y V 1 x,y 0 X |
Период свободных колебаний груза,
подвешенного на упругой нити:
T = 6, 28* Ö(M/Kn). Примем dt = T/300.
Проекции ускорения определяются как дискретная функция расстояния " r " от начала координат до точки закрепления нити: если r <= L, то ускорение от сил упругости равно нулю, в остальных случаях:
Ax = -x*Ky*dr/(r*M);
Ay = -y*Ky*dr/(r*M) - 9.81; где dr = (r-L) > 0.
Проекцию ускорения на ось “Х” от сил упругости, запишем в виде функции:
FUNCTION FA(x, r, L, Kn, M: double): double;
begin if (r-L)>0 then FA:= -x*Kn*(r-L)/(r*M) else FA:= 0 end;
Аналогичная функция составляется для проекции ускорения на ось “У”. Методика расчета соответствует приведенной для движения спутника в поле тяготения планеты.
Практическое задание N 2. 26
1. Построить траекторию движения мяча, подвешенного на упругой нити в вязкой среде, рассчитанную разностным моделированием. Сопротивление среды пропорционально скорости движения мяча: kc=0. 01, с -1 . Нить закреплена в центре квадрата со стороной 2*Lm, длина нити L=1, м, коэффициент упругости Kn=5, н/м. Масса мяча M=0. 2, кг. Мяч начинает движение из точки с координатами x 1 =-0. 5*L, y 1 =0, со скоростью V 1 =10, м/с, под углом 45 0 .
2. Построить траекторию движения мяча, подвешенного на упругой нити в квадратной коробке, рассчитанную разностным моделированием, с учетом уменьшения нормальной составляющей скорости на 20% при отражении мяча от стенки. Сопротивление среды пропорционально скорости движения мяча: kc=0. 05, с -1 . Нить длиной L=1, м, закреплена в центре квадрата со стороной a=1. 5*L. Коэффициент упругости Kn=5, н/м, масса мяча M=0. 1, кг. Мяч начинает движение из точки с координатами x 1 =-L, y 1 =0, со скоростью V 1 x=1, м/с, V 1 y=5, м/с.
2. 4. Моделирование многовариантных задач с использованием графов
| |
Рассмотрим "классический" пример многовариантной задачи. Пусть пункты A и B связаны между собой дорогами, могущими проходить также через пункты 1, 2, 3,..., N. В общем случае каждый пункт связан дорогами со всеми остальными. В частном случае некоторые связи (дороги) отсутствуют. Схематически эти пункты и связи можно изобразить в виде графа.
Графом называется совокупность узлов (пункты A, B, 1, 2, . . . , N) и связывающих их ребер (дорог). Маршрутом движения называется последовательность связанных ребрами узлов. В дальнейшем будем рассматривать те маршруты движения, которые всегда начинаются из пункта A и заканчиваются в пункте B. Причем пункты A и B на маршруте повторяться не могут. Например: А-1-4-В .
Ставится задача составить маршруты при заданных ограничениях (фильтрах), либо найти оптимальный по некоторым параметрам маршрут и т. д. Например, известна стоимость проезда по каждой из дорог. Необходимо найти маршрут с наименьшей стоимостью проезда, либо найти все маршруты со стоимостью не превышающей определенную величину и т. д.
Пусть узел A имеет номер "0", а узел B - номер "N+1". Рассмотрим общий случай: каждый пункт связан со всеми остальными. Обозначим M - число промежуточных узлов на маршруте.
При М = 0 маршрут может проходить только из узла "0" в узел "N+ 1".
При М = 1 маршрут проходит через один из узлов: j1= 1, либо j1= 2, .., либо j1= N.
При М = 2 маршрут проходит через два узла, причем первый из них может иметь номер: j1=1, либо j1=2, ... либо j1=N, а второй - номер: j2=1, либо j2=2, ... либо j2=N, т. е. возможно N 2 маршрутов. Графически все маршруты можно представить в виде:
![]()
![]() A M=1 A M=2
A M=1 A M=2
1 . . . j1 . . . N
![]()
![]()
![]() 1 2 3 ... j1 ... N 1 2 3 ... j2 . N 1 2 3 ... j2 ... N 1 2 3 ... j2 .. N
1 2 3 ... j1 ... N 1 2 3 ... j2 . N 1 2 3 ... j2 ... N 1 2 3 ... j2 .. N
 |
Таким образом, число маршрутов равно N M и время перебора маршрутов при больших значениях N и M очень быстро растет.
При постановке задачи нахождения маршрутов указывается значение M - наименьшее число узлов на маршруте, M1 - наибольшее число узлов на маршруте. Причем 1<=M<=M1. Например, пусть на графе имеется три узла N=3 и необходимо составить маршруты, проходящие через два узла, т. е. M=2, M1=2. Тогда в общем случае имеются маршруты:
0-1-1-4; 0-2-1-4; 0-3-1-4; односторонняя связь
0-1-2-4; 0-2-2-4; 0-3-2-4; 1 2 3
0-1-3-4; 0-2-3-4; 0-3-3-4; двусторонняя связь
Постановка задачи нахождения маршрутов включает определение матрицы коэффициентов aij, характеризующих связи между узлами i и j. Связь узла A задается коэффициентами a 0 j, узла В - коэффициентами ai N+ 1 . Матрица имеет вид:
a 11 a 12 a 13 ... a 1N Если aij = aji = 0, то связь
a 21 a 22 a 23 ... a 2N между узлами i и j отсутствует.
a 31 a 32 a 33 ... a 3N Если aij=0 и aji<>0, то связь
........................... . между узлами i и j односторонняя.
a N1 a N2 a N3 ... a NN Если aij<>0 и aji<>0, то связь
между узлами i и j двусторонняя.
Если aij = aji при i =1, 2, . . , N; j = 1, 2, . . , N, то матрица симметричная.
Если aij = 0 при j =1, 2, . . , N; i > j, то матрица треугольная.
Значение aij может содержать значение ребра, связывающего узлы i и j (например, стоимость проезда), либо значение, содержащееся в узле i или j, либо любое значение, указывающее на существование связи между узлами i и j.
Введем линейный массив "Y", коэффициенты которого обозначают номера узлов графа через которые проходит маршрут, а индексы показывают номер пункта по порядку следования на маршруте. Операторы по перебору маршрутов имеют вид:
Y:=0; {номер узла "А" графа}
repeat {цикл по числу узлов на маршруте}
for j:= 1 to M do Y[j]:=1; {начальные номера узлов на маршруте}
Y:=N+1; {номер узла "B" графа}
repeat {цикл по перебору номеров узлов на маршруте}
for j:=1 to M+1 do if a,y[j]]=0 then goto METKA; {проверка}
{****** здесь ставятся операторы фильтра ************}
{****** . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . ************}
for j:=0 to M+1 do write("-", Y[j]); writeln; {вывод маршрута}
METKA: Y:=Y+1; {изменение номера узла первого пункта на маршруте}
for j:=1 to M-1 do {определяем номера узлов на маршруте}
if Y[j]>N then begin Y[j]:=1; Y:=Y+1 end else Break;
until Y[M]=N+1;
until M>M1;
В начале программы задается возможный маршрут 0-1-1-1-. . . -1-N+1 для заданного значения M>0. Проверяется наличие связей и ставятся фильтры для определения маршрута. Затем увеличивается номер узла первого пункта по порядку следования на маршруте: 0-2-1-1-. . . -1-N+1 и т. д. до 0-N-1-1-. . . -1-N+1. При превышении номера узла значения N, номер узла сбрасывается до единицы, а номер следующего узла увеличивается на единицу: 0-1-2-1-. . . -1-N+1 и снова увеличивается номер узла первого пункта до значения N: 0-N-2-1-. . . -1-N+1 и далее сбрасывается до единицы с увеличением номера следующего узла: 0-1-3-1-. . . -1-N+1. После (N-1)-го сброса и увеличения значения узла первого пункта до N получим маршрут: 0-N-N-1-. . . -1-N+1 и далее: 0-1-1-2-. . . -1-N+1. Таким образом, происходит перебор всех возможных маршрутов до 0-N-N-N-. . . -N-N+1. После этого рассматриваются маршруты для M=M+1 включая M=M1. Отметим, что при необходимости маршрут 0-N+1 для M=0 нужно рассмотреть отдельно.
При решении конкретных задач необходимо определить значение коэффициентов aij матрицы связи и установить необходимые фильтры.
Рассмотрим задачуопределения стоимости маршрутов из A в B .
1.) Зададим стоимость проезда из узла i в узел j:
for i:=0 to N+1 do for j:=i to N+1 do a:=Random(X); {X-дано}
for i:=0 to N+1 do a:=0; { движение внутри узла запрещено}
for i:=0 to N+1 do for j:=i to N+1 do a:=a; {связи }
{двусторонние и равнозначные}
2). Матрицу связей можно вывести на экран для проверки. При выводе маршрута на экран или в файл можно выводить также значение стоимости маршрута.
S:=0; for m:=1 to M1+1 do S:=S+a,y[m]]; {стоимость маршрута}
| 1 2 3 4 5 6 7 8 9 |
Рассмотрим задачу расстановки мин на прямоугольном поле размером Nx*Ny. При этом M=M1=N=Nx*Ny и все узлы должны быть пройдены без повторений. Расстановка начинается из узла с заданным номером NH и может закончиться в узлах на верхней границе.
1) Определим матрицу связей:
for i:=0 to N+1 do for j:=1 to N+1 do a:=0;
for i:=1 to N-1 do begin a:=1; a:=1 end; {связи по гориз}
for j:=1 to Ny-1 do begin k:=Nx*j; a:=0; a:=0 end;
for i:=1 to Nx do for j:=1 to Ny-1 do {связи по вертикали}
begin k:=Nx*(j-1)+i; a:=1; a:=1 end;
a:=2; { NH - узел связи c узлом 0}
for i:=1 to Nx do a:=3; { 1, . . , Nx - узлы связи c узлом N+1}
2). Установим фильтр, запрещающий возврат в узел на маршруте:
for k:=1 to M do c]:=0; for k:=1 to M do
begin c]:=c]+1; if c]=1 then goto METKA end;
Здесь производится суммирование повторяющихся номеров узлов на маршруте. При совпадении номера узла значение счетчика c]=1 -маршрут не рассматривается.
![]() Рассмотрим задачу загрузки N - видов коробок
в машину. Задается число коробок каждого вида: Ki, их вес Mi и объем Vi, где i=1, 2, . . , N. Ограничения могут быть по общему весу и объему. Число узлов графа равно N. Число узлов на маршруте M=1, М1=K 1 +K 2 +. . . +K N . Интервал М-М1 можно уменьшить просчитав наибольшее допустимое по весу и объему число коробок KMi каждого вида загружаемых в машину (KMi<=Ki). Тогда М = min(KMi), а М1 = max(KMi). Поскольку порядок загрузки не имеет значения, то все связи односторонние. 0
Рассмотрим задачу загрузки N - видов коробок
в машину. Задается число коробок каждого вида: Ki, их вес Mi и объем Vi, где i=1, 2, . . , N. Ограничения могут быть по общему весу и объему. Число узлов графа равно N. Число узлов на маршруте M=1, М1=K 1 +K 2 +. . . +K N . Интервал М-М1 можно уменьшить просчитав наибольшее допустимое по весу и объему число коробок KMi каждого вида загружаемых в машину (KMi<=Ki). Тогда М = min(KMi), а М1 = max(KMi). Поскольку порядок загрузки не имеет значения, то все связи односторонние. 0
![]() 1 2 ... k ... N N+1
1 2 ... k ... N N+1
1) Определим матрицу связей:
for i:=0 to N+1 do for j:=i to N+1 do a:=0; {нижний треугольник}
for i:=0 to N+1 do for j:=i to N+1 do a:=1; {верхний треугольник}
2) Определение числа коробок каждого вида аналогично суммированию повторяющихся номеров узлов на маршруте.
Практическое задание N 2. 27
1) Вывести в файл стоимость маршрутов без повторяющихся узлов при N=4, M=3, M1=4, Х=9. Определить номера маршрутов с наименьшей и наибольшей стоимостью
для разных значений М.
2) Вывести символами псевдографики в текстовом режиме маршруты движения в прямоугольнике 2х4, либо 4х2. Начало движения при NH=8.
3) Вывести общий вес и число коробок каждого из 3-х видов, загружаемых в машину. Задать веса функцией Random(50)+50; Установить фильтр по общему весу G<900. Общее число коробок: M=10, M1=12.
Под объектом моделирования понимают любой предмет, процесс или явление, которые изучают методом моделирования. При изучении объекта учитываются только те свойства, которые необходимы для достижения цели. Выбор свойств объекта при построении модели является важной задачей на первых этапах моделирования.
Модель объекта –
это:
1) такая мысленно представимая или материально реализованная система, которая, отображая или воспроизводя объект исследования, способна заменить его так, что её изучение даёт новую информацию об объекте.
2) объект - заместитель, который учитывает реальные свойства объекта, необходимые для достижения цели.
Основная функция модели – не только описание объекта, но и получение информации о нём.
Различают физическое и математическое моделирование.
Физи́ческое модели́рование - метод экспериментального изучения различных физических явлений, основанный на их физическом подобии . Метод применяется при следующих условиях:
- Исчерпывающе точного математического описания явления на данном уровне развития науки не существует, или такое описание слишком громоздко и требует для расчётов большого объёма исходных данных, получение которых затруднительно.
- Воспроизведение исследуемого физического явления в целях эксперимента в реальных масштабах невозможно, нежелательно или слишком дорогостояще (например, цунами).
В широком смысле, любой лабораторный физический эксперимент является моделированием, поскольку в эксперименте наблюдается конкретный случай явления в частных условиях, а требуется получить общие закономерности для всего класса подобных явлений в широком диапазоне условий. Искусство экспериментатора заключается в достижении физического подобия между явлением, наблюдаемым в лабораторных условиях и всем классом изучаемых явлений.
Математическое моделирование , в широком смысле, включает исследования не только с помощью чисто математических моделей. Здесь используются также информационные, логические, имитационные и другие модели и их комбинации. В этом случае математическая модель представляет собой алгоритм, включающий определение зависимости между характеристиками, параметрами и критериями расчета, условия протекания процесса функционирования системы и т.д. Данная структура может стать моделью явления, если она с достаточной степенью отражает его физическую сущность, правильно описывает соотношение свойств и подтверждается результатами проверки. Применением математических моделей и вычислительной техники реализуется один из наиболее эффективных методов научных исследований - вычислительный эксперимент, позволяющий изучать поведение сложных систем, которые трудно физически смоделировать. Часто это связано с большой сложностью и стоимостью объектов, а в некоторых случаях невозможностью воспроизвести эксперимент в реальных условиях.
Эффективность применения информационных систем в сфере образования. Задачи, решаемые ИС в сфере образования. Специфика информационных потребностей преподавательского и управленческого персонала сферы образования. Основные показатели качества информационного обеспечения сферы образования и обоснование требований к их количественным значениям
В современном обществе применение информационных технологий во всех сферах жизнедеятельности стало обязательным сопровождающим компонентом. Особенно важная роль её применению отводится в области познания, изучения, т.е. в сфере образования. ИТ-технологии занимают одно из ведущих мест в интеллектуализации человека и общества в целом, повышении культурного и образовательного уровня каждого гражданина.
В последнее время в сфере образования информационные технологии, основанные на новейших компьютерных и аудиовизуальных достижениях науки и техники, находят все большее применение. Одним из эффективных направлений реализации образовательных услуг является использование различных форм обучения на основе информационных и обучающих технологий.
Помимо этого, стремление активно применять современные информационные технологии в сфере образования необходимо ориентировать на повышение уровня и качества подготовки специалистов. С каждым годом растет количество организаций и предприятий обращающихся на рынок образовательных услуг. В связи с этим в самых благоприятных условиях оказываются те учебные заведения, которые включают в себя довузовское, вузовское и послевузовское образование с использованием новых образовательных технологий.
В настоящее время все более возрастает роль информационно-социальных технологий в образовании, которые обеспечивают всеобщую компьютеризацию учащихся и преподавателей на уровне, позволяющем решать, как минимум, три основные задачи:
– обеспечение выхода в сеть Интернет каждого участника учебного процесса, причем, желательно, в любое время и из различных мест пребывания;
– развитие единого информационного пространства образовательных индустрий и присутствие в нем в различное время и независимо друг от друга всех участников образовательного и творческого процесса;
– создание, развитие и эффективное использование управляемых информационных образовательных ресурсов, в том числе личных пользовательских баз и банков данных и знаний учащихся и педагогов с возможностью повсеместного доступа для работы с ними.
Основными преимуществами современных информационных технологий являются: наглядность, возможность использования комбинированных форм представления информации - данные, стереозвучание, графическое изображение, анимация, обработка и хранение больших объемов информации, доступ к мировым информационным ресурсам, которые должны стать основой поддержки процесса образования.
Необходимость усиления роли самостоятельной работы обучаемого требует внесения существенные изменений в структуру и организацию учебного процесса, повышению эффективности и качества обучения, активизации мотивации познавательной деятельности в ходе изучения теоретического и практического учебного материала по той или иной дисциплине.
В процессе информатизации образования необходимо иметь в виду, что главный принцип использования компьютера - это ориентация на те случаи, когда человек не может выполнить поставленную педагогическую задачу. Например, преподаватель не может наглядно продемонстрировать большинство физических процессов без компьютерного моделирования.
С другой стороны, компьютер должен помогать развитию творческих способностей учащихся, способствовать обучению новым профессиональным навыкам и умениям, развитию логического мышления. Процесс обучения должен быть направлен не на умение работать с определенными программными средствами, а на совершенствование технологии работы с различной информацией: аудио- и видео-, графической, текстовой, табличной.
Современные мультимедиа технологии и инструментальные средства позволяют реализовать всю гамму компьютерных обучающих программ. Однако их использование требует от преподавателей достаточно высокой квалификации пользователя.
ВИДЫ ХИМИЧЕСКИХ РЕАКТОРОВ
Химический реактор - устройство, предназначенное для проведения в нем химических превращений.
Химический реактор - понятие обобщенное, относится к реакторам, колоннам, башням, автоклавам, камерам, печам, контактным аппаратам, полимеризаторам, гидрогенизаторам, окислителям и другим аппаратам, названия которых происходят из-за их назначения или даже внешнего вида. Общий вид реактора и схемы некоторых из них приведены на рис. 4.1.
Емкостной реактор / оснащен мешалкой, которая перемешивает реагенты (чаще жидкости, суспензии), помещаемые внутрь аппарата. Температурный режим поддерживается с помощью теплоносителя, циркулирующего в рубашке реактора или во встроенном в него теплообменнике. После проведения реакции продукты выгружают, и после очистки реактора цикл повторяется. Процесс периодический.
Емкостной реактор 2 является проточным, т.к. реагенты (чаще газ, жидкость, суспензия) непрерывно проходят через него. Газ барботирует через жидкость.
Колонный реактор 3 характеризуется отношением высоты к диаметру. которое для промышленных реакторов составляет 4-6 (в емкостных реакторах это отношение около 1). Взаимодействие газа и жидкости такое же, как в реакторе 2
Насадочный реактор 4оснащен кольцами Рашига или другими небольшими элементами - насадкой. Взаимодействуют газ и жидкость. Жидкость стекает по насадке, а газ движется между элементами насадки.
Реакторы 5-8 в основном используют дня взаимодействия газа с твердым реагентом.
В реакторе 5твердый реагент неподвижен, газообразный или жидкий реагент непрерывно проходит через него. Процесс - периодический по твердому веществу.
Реакторы 6~ 8 модифицированы таким образом, чтобы и по твердому реагенту процесс являлся непрерывным. Твердый реагент продвигается вдоль вращающегося наклонно установленного круглого реактора били просыпается через реактор 7. В реакторе 8 газ подастся снизу под большим давлением так, что твердые частицы оказываются во взвешенном состоянии, образуя псевдоожиженный, или кипящий, слой, обладающий некоторыми свойствами жидкости.
Трубчатый реактор 9 по виду подобен кожухотрубному теплообменнику. Через трубки, в которых протекает реакция, проходят газообразные или жидкие реагенты. Обычно в трубки загружен катализатор. Температурный режим обеспечивают циркуляцией теплоносителя в межтрубном пространстве.
Реакторы 5 и 9 используют также для проведения процессов на твердом катализаторе.
Трубчатый реактор 10 часто применяют для осуществления высокотемпературных гомогенных реакций, в том числе в вязкой жидкости (например, пиролиз тяжелых углеводородов). Нередко такие реакторы называют печами.
Многослойный реактор 11 оснащен системой, позволяющей охлаждать или нагревать реагент, находящийся между несколькими слоями твердого вещества, выполняющего роль, например, катализатора. На рисунке показано охлаждение исходного газообразного вещества холодным газом, введенным между верхними слоями катализатора, и теплоносителем через систему теплообменников, помещенных между другими слоями катализатора.
Многослойный реактор 12 предусмотрен для проведения в нем газожидкостных процессов.
Приведенные на рис. 4.1 схемы отображают лишь часть примяеых в промышленности реакторов. Однако проведенная далее систематизация конструкций реакторов и протекающих процессов, позволяет разобраться и провести исследование в любом из них.
Для всех реакторов характерны общие структурные элементы, представленные в реакторе на рис. 4.2, аналогичном 11 -му на рис. 4.1.
Реакционную зону 7, в которой протекает химическая реакция, представляют несколько слоев катализатора. Она есть во всех реакторах: в реакторах 1-3 на рис. 4.1 - это слой жидкости, в реакторах 4, 5, 7 - слой насадки или твердого компонента, в реакторах 6, 8 - часть объема реактора с твердым компонентом, в реакторах 9, 10 - внутренний объем трубок, где протекает реакция.
Исходная реакционная смесь подается через верхний штуцер. Чтобы обеспечить равномерно распределенное прохождение газа через реакционную зону, обуславливающее однородный контакт реагентов, установлен распределитель потока. Эго - устройство ввода 2. В реакторе 2 на рис. 4.1 распределителем газа является барботер, в реакторе 4 - разбрызгиватель.
Между первым сверху и вторым слоями два потока смешиваются в смесителе 3. Между вторым и третьим слоями помещен теплообменник 4. Эти структурные элементы предназначены для изменения состава и температуры потока между реакционными зонами. Теплообмен с реакционной зоной (отвод теплоты, выделяющейся в результате протекания экзотермических реакций или подогрев реагирующей смеси) осуществляется через поверхность встроенных теплообменни-

ков или через внутреннюю поверхность рубашки реактора (аппарат 1 на рис. 4.1), либо через стенки труб в реакторах Р, 10. Реактор может быть оснащен устройствами разделения потоков.
Продукты выводятся через выходное устройство 5.
В теплообменниках и устройствах ввода, вывода, смешения, разделения, распределения потоков протекают физические процессы. Химические реакции осуществляются в основном в реакционных зонах, которые будут дальнейшим объектом исследования. Процесс, происходящий в реакционной зоне, представляет собой совокупность част ных этапов, которые схематически показаны на рис. 4.3 для каталитического и газожидкостного взаимодействия.
Рис. 4.3, а представляет схему реакционного процесса с участием катализатора, через неподвижный слой которого проходит общий

(конвективный) поток газообразных реагентов (7). Реагенты диффундируют к поверхности зерен (2) и проникают в поры катализатора (3 ), на внутренней поверхности которых протекает реакция (4 ). Образующиеся продукты реакции обратным путем отводятся в поток. Выделяющаяся в результате химического превращения теплота за счет теплопроводности переносится по слою (5), а от слоя через стенку - к хладагенту (б). Возникающие градиенты концентраций и температуры вызывают дополнительные потоки теплоты и вещества (7) к основному конвективному движению реагентов в слое.
На рис. 4.3, б представлен процесс в слое жидкости, через который барботирует газ. Между пузырями (/) газа и жидкостью происходит массообмен реагентами (2 ). Динамика жидкости складывается из движения около пузырей (.?) и циркуляции в масштабе слоя (4). Первое - подобно турбулентной диффузии, второе аналогично циркуляционному конвективному движению жидкости через реакционную зону. В жидкости и, в общем случае, в газе протекает химическое превращение (5).
Приведенные примеры показывают сложную структуру процессов, протекающих в реакционной зоне. Если учесть множество схем и конструкций существующих реакторов, то разнообразие процессов в них многократно возрастает". Необходим научный метод, позволяющий систематизировать это многообразие, найти общность в нем, выработать систему представлений о закономерностях явлений и связей между ними, т.е. создать теорию химических процессов и реакторов. Такой научный метод рассмотрен далее.
4. Использование методов и принципов системного исследования при разработке ХТС
4.2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
КАК МЕТОД ИССЛЕДОВАНИЯ ХИМИЧЕСКИХ ПРОЦЕССОВ И РЕАКТОРОВ
Модель и моделирование. Моделирование - метод исследования объекта (явления, процесса, устройства) на модели - давно используется в различных областях науки и техники с целью исследования самого объекта исследованием его модели. Полученные свойства модели переносят на свойства моделируемого объекта.
Модель - специально созданный для изучения объект любой природы, более простой, чем исследуемый, по всем свойствам, кроме тех, которые надо изучить, и способный заменить исследуемый объект так, чтобы получить новую информацию о нем.
Учитываемые в каждой модели явления и параметры называются составляющими модели.
Для изучения разных свойств объекта может быть создано несколько моделей, каждая из которых отвечает определенной цели исследования, однако и одна модель может дать необходимую информацию о нескольких изучаемых параметрах, тогда можно говорить о единстве «цель-модель». Если модель отражает большее (или меньшее) число свойств, то она называется широкой (или узкой). Используемое иногда понятие «общая модель» как отражающая псе свойства объекта - бессмысленно по сути.
Чтобы достигнуть поставленной цели, изучаемая модель должна быть подвергнута влиянию те же факторов, что и объект. Составляющие и параметры процесса, влияющие на изучаемые свойства, называются существенными составляющими модели. Изменение некоторых параметров может очень слабо влиять на свойства объекта. Такие составляющие и параметры называют несущественными, и их можно не учитывать в построении модели. Соответственно, простая модель содержит лишь существенные составляющие, иначе модель будет избыточной, поэтому простая модель не есть простая по внешним признакам (например, несложная по структуре или конструкции). Но если в модель входят не все составляющие, существенно влияющие на изучаемые свойства, то она будет неполной , и результаты ее исследования могут не точно предсказать поведение реального объекта. В этом и заключается творчество и научный подход к построению модели - выделить именно те явления и учесть именно тс параметры, которые являются существенными для изучаемых свойств.
Кроме предсказания заданных свойств, модель должна давать информацию о неизвестных свойствах объекта. Это может быть достигнуто лишь в том случае, если модель является простой и полной, тогда в ней могут проявиться новые свойства.
Физическое и математическое моделирование
Пример физического моделирования - исследование обтекания самолета воздухом на модели в аэродинамической трубе.
В таком методе исследования устанавливается подобие явлений (процессов) в объектах разного масштаба, основанное на количественной связи между величинами, характеризующими эти явления. Такими величинами являются: геометрические характеристики объекта (форма и размеры); механические, теплофизические и физико-химические свойства рабочей среды (скорость движения, плотность, теплоемкость, вязкость, теплопроводность и др.); параметры процесса (гидравлическое сопротивление, коэффициенты теплопередачи, массооб- мена и др.). Развитая теория подобия устанавливает между ними определенные отношения, называемыми критериями подобия. Обычно их обозначают начальными буквами имен известных ученых и исследователей (например, Re - критерий Рейнольдса, Nu - критерий Нус- сельта, Аг - критерий Архимеда). Для характеристики какою-либо явления (теплоотдачи, массопереноса и т.д.) устанавливаются зависимости между критериями подобия - критериальные уравнения.
Физическое моделирование и теория подобия нашли широкое применение в химической технологии при исследовании тепловых и диффузионных процессов. Критериальные уравнения для расчета некоторых параметров тепло- и массопереноса буду!" использованы далее.
Попытки использования теории подобия для химических процессов и реакторов оказались неудачными вследствие ограниченности ее применения. Причины заключаются в следующем. Химическое превращение зависит от явлений переноса теплоты и вещества, так как они создают соответствующие температурные и концентрационные условия в месте проведения реакции. В свою очередь, химическая реакция изменяет состав и теплосодержание (и, соответственно, темпе ратуру) реагирующей смеси, что изменяет перенос теплоты и вещества. Таким образом, в реакционном технологическом процессе участвуют химическая (превращение веществ) и физическая (перенос) его составляющие. В аппарате небольшого размера выделяющаяся теплота реакции легко теряется и слабо влияет на скорость превращения, поэтому основной вклад в результаты процесса вносит химическая составляющая. В аппарате же большого размера выделяющаяся теплота «запирается» в реакторе, существенно изменяя поле температур и, следовательно, скорость и результат протекания реакции. Следовательно
химические и физические составляющие реакционного процесса к целом зависят от масштаба.
Другой причиной является несовместимость условий подобия дня химических и физических составляющих процесса в реакторах разного масштаба. Например, превращение реагентов зависит от времени пребывания их в реакторе, равного отношению размера аппарата к скорости потока. Условия тепло- и массопсреноса, как следует из теории подобия, зависят от критерия Рейнольдса, пропорционального произведению размера аппарата на скорость потока. Сделать одинаковыми в аппаратах разною масштаба и отношение, и произведение двух величин (в данном примере размера и скорости) невозможно.
Трудности масштабного перехода объекта к модели для реакционных процессов удается преодолеть, используя математическое моделирование, в котором модель и объект имеют разную физическую природу, но одинаковые свойства. Например, механический маятник и замкнутый электрический контур, состоящий из конденсатора и катушки индуктивности, имеют разную физическую природу, но одинаковое свойство: колебание (механическое и электрическое соответственно).
Свойства этих устройств описываются одним и тем же уравнением колебания:
![]() .
.
Отсюда и название вида моделирования - математическое. Пара метры устройств (l M /g - для маятника и LC - для электрического контура), можно подобрать таким образом, чтобы колебания по частоте были одинаковыми. Тогда электрический колебательный контур будет моделью маятника. Также можно исследовать решение приведенного уравнения и предсказать свойства маятника. Соответственно, математические модели подразделяются на реальные , представленные неким физическим устройством, и знаковые, представленные математическими уравнениями. Классификация моделей представлена на рис. 4.4.
Для построения реальной математической модели необходимо сначала создать знаковую, и обычно математическую модель отождествляют с уравнениями, описывающими объект. Универсальной реальной математической моделью является электронная вычислительная

машина (ЭВМ). По уравнениям, описывающим объект, ЭВМ «настраивают» (программируют), и ее «поведение» будет описываться этими уравнениями. Далее именно знаковую математическую модель будем называть математической моделью процесса.
О подобии математических моделей разных процессов. Как уже было показано, процессы движения механического маятника и изменения силы тока в электрическом контуре могут быть представлены одинаковыми математическими моделями, т.е. описываться одним и тем же дифференциальным уравнением второго порядка. Решение этого уравнения есть функция х(/), которая указывает на колебательный вид движения этих разных по природе объектах. Из решения уравнения также можно определить изменение во времени положения маятника относительно вертикальной оси или изменение во времени направления тока и его величины. Это - интерпретация свойств математической модели на показатели изучаемых объектов. 13 этом проявляется весьма полезная особенность математического моделирования. Подобными математическими моделями могут быть описаны разные процессы. Такая «универсальность» математической модели проявляется в исследовании, например, процессов в емкостном J и трубчатом 9 реакторах на рис. 4.1 (см. разд. 4.1), изучении взаимодействия газообразного реагента с твердой частицей и гетерогенно -каталитического процесса (разд. 4.5.2 и 4.5.3), рассмотрении критических явлений на единичном зерне катализатора и в объеме реактора
Математическое моделирование химических происссов и реакторов . В
обшем виде математическое моделирование реакторов можно представить в виде схемы, изображенной на рис. 4.5. Поскольку в различных по масштабу реакционных процессах влияние физических и химических составляющих (явлений) на реакционный процесс различное, выявление этих явлений и их взаимодействие - анализ - наиболее существенный момент в математическом моделировании химических процессов и реакторов. Следующим этапом является определение термодинамических и кинетических закономерностей для химических превращений (химические явления), параметров явлений переноса (физические явления) и их взаимодействие. Для этого используют данные экспериментальных исследовании, математическое моделирование не исключает эксперимент, а активно его использует, но эксперимент прецизионный, направленный на исследование закономерностей отдельных составляющих процесса. Результаты анализа процесса и исследования его составляющих позволяют построить математическую модель процесса (этап синтез па рис. 4.5) - уравнения, описывающие его. Модель создается на основе фундаментальных законов природы, например, сохранения массы и энергии, полученных сведений об отдельных явлениях и установленных взаимодействиях между ними. Исследование модели направлено па изучение ее свойств, при этом используется математический аппарат качественного анализа и вычислительные методы, или, как говорят, проводится вычислительный эксперимент. Полученные свойства модели далее следует интерпретировать как свойства изучаемого объекта, которым в данном случае является химический реактор. Например, математическую зависимость у(т) необходимо представить в виде изменения концентрации веществ по длине реактора или во времени, а несколько корней уравнения интерпретировать как неоднозначность режимов и т.д.
Тем нс менее, даже приблизительная схема процесса в слое катализатора (рис. 4.3) включает довольно много составляющих, соответственно модель процесса будет довольно сложная, и сс анализ неоправданно усложнен. Для сложного объекта (процесса) используется специальный подход к построению модели, заключающийся в его разделении на ряд более простых операций, различающихся масштабом. Например, в каталитическом процессе выделяются: реакция на поверхности зерна, процесс на одиночном зерне катализатора и процесс в слое катализатора.
Каталитическая реакция - сложный многостадийный процесс, протекающий в масштабе размера молекул. Скорость реакции определяется условиями ее протекания (концентрация и температура) и не зависит от того, где такие условия созданы: в реакторе малого или большого размера, - т.е. не зависит от масштаба всего процесса. Изу
чение сложного механизма реакции позволяет построить ее кинетиче скую модель - уравнение зависимости скорости реакции от условий ее протекания. Понятно, что эта модель будет значительно проще, чем система уравнений всех стадий реакции, и ее исследование будет информативным.
Процесс на отдельном зерне катализатора, размером несколько миллиметров, включает реакцию, представленную сс кинетической моделью, и перенос вещества и теплоты в порах зерна и между его наружной поверхностью и обтекающим потоком. Превращение на зерне определяется условиями протекания процесса - составом, температурой и скоростью обтекающего потока и не зависит от того, где созданы такие условия - в реакторе малого или большого размера, т.е. не зависит от масштаба всего процесса. Анализ полученной модели позволяет получить свойства процесса, например, скорости превращения в виде зависимости только от условий его протекания - наблюдаемую скорость превращения.
Процесс в слое катализатора включает процесс на зерне, для которого закономерности уже выявлены, и перенос теплоты и вещества в масштабе слоя.
Выделение в сложном процессе простых этапов, различающихся масштабом протекания, позволяет построить иерархическую систему моделей , каждая из которых имеет свой масштаб и, главное, свойства такой системы не зависят от масштаба всего процесса (инвариантны к масштабу).
В общем виде модель реакционного процесса, построенную по иерархическому принципу можно представить схемой (рис. 4.6).
Химическая реакция, состоящая из элементарных стадий, протекает в молекулярном масштабе. Ее свойства (например, скорость) не зави сят от масштаба реактора, т.е. скорость реакции зависит только от условий ее протекания независимо от того, как или где они созданы. Результатом исследования на этом уровне является кинетическая модель химической реакции - зависимость скорости реакции от условий. Следующий масштабный уровень - химический процесс - совокупность химической реакции и явлений переноса, таких как: диффузия и теплопроводность. На этой стадии кинетическая модель реакции является одной из составляющих процесса, причем объем, в котором рассматривается химический процесс, выбирается с такими условиями, чтобы закономерности его протекания не зависели от размера реактора. Например, это может быть рассмотренное выше зерно катализатора. Далее полученная модель химического процесса как одна из составляющих элементов, в свою очередь, входит в следующий масштабный уровень - реакционную зону, в которую также входят и структурные закономерности потока, и явления переноса в сс масштабе. И,

наконец, в масштабе реактора в составляющие процесса входят реакционная зона, узлы смешения, теплообмена и др. Таким образом, математическая модель процесса в реакторе представлена системой математических моделей разного масштаба.
Иерархическая структура математической модели процесса в реакторе позволяет:
7) полностью описывать свойства процесса путем детального исследования его основных этапов разного масштаба;
8) проводить изучение сложного процесса по частям, применяя к каждой из них специфические, прецизионные методы исследования, что повышает точность и надежность результатов;
9) устанавливать связи между отдельными частями и выяснять их роль в работе реактора в целом;
10) облегчить изучение процесса на более высоких уровнях;
11) решать задачи масштабного перехода.
При дальнейшем изложении материала, изучение процесса в химическом реакторе будет проводиться с помощью математического моделирования.
Похожая информация.
- Граница между европой и азией Америка относится к европе
- Как экономить деньги при маленькой зарплате?
- Порядок получения жилищной субсидии для военнослужащих
- Лимит кассы: нормативная база и сроки установления лимита
- Полная система вычетов Алгебраическая форма комплексного числа
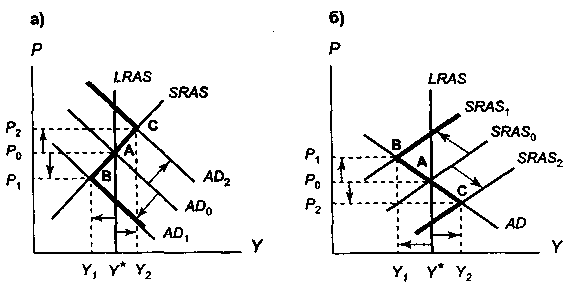
- Модель «Совокупный спрос – совокупное предложение Увеличение совокупного спроса вызывает
- Что называется периодом в физике
- Виды и типы недвижимости, их экономическая составляющая Поля инициализаторов типа
- Экономика, население и города Чеченской Республики
- Особенности проведения региональной программы материнский капитал в московской области Региональный материнский капитал программе семья
- Должностная инструкция страхового агента росгосстрах
- Учет материалов на складе и в бухгалтерии
- На вопрос «Можно ли строить дом без разрешения на строительство?
- Ип на осно какие налоги платит?
- Доходы и расходы будущих периодов Как распределить расходы, затрагивающие несколько налоговых периодов
- Экономические циклы, их особенности и виды
- Необходимо знать от чего зависят цены на жилье
- Контрольная работа: Экономическая мысль Древней Греции
- Бухгалтерские проводки по реализации товаров и услуг 1с бухгалтерия 8
- Оборотные активы организации