Оптимальное распределение инвестиций методом линейного программирования. Распределение инвестиций методом динамического программирования
Динамическое программирование представляет собой математический аппарат, разработанный для эффективного решения некоторого класса задач математического программирования. Этот класс характеризуется возможностью естественного (а иногда и искусственного) разбиения всей операции на ряд взаимосвязанных этапов. Термин "динамическое" в названии метода возник, видимо, потому что этапы предполагаются разделенными во времени. Однако этапами могут быть элементы операции, никак не связанные друг с другом показателем времени. Тем не менее, метод решения подобных многоэтапных задач применяется один и тот же, и его название стало общепринятым, хотя в некоторых источниках его называют многоэтапным программированием.
Модели динамического программирования могут применяться, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капиталовложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т.д.
Для определения сущности динамического программирования рассмотрим задачу:
Представим себе некоторую операцию О, состоящую из ряда последовательных "шагов" или этапов, например, деятельность отрасли промышленности в течение ряда хозяйственных лет. Пусть число шагов равно m. Выигрыш (эффективность операции) Z за всю операцию складывается из выигрышей на отдельных шагах:
где zi- выигрыш на i-м шаге.
Если Z обладает таким свойством, то его называют аддитивным критерием.
Операция О является управляемым процессом, то есть мы можем выбирать какие-то параметры, которые влияют на его ход и исход, причем на каждом шаге выбирается решение, от которого зависит выигрыш и на данном шаге, и выигрыш за операцию в целом. Эти решения называются шаговыми.
Совокупность всех шаговых управлений является управлением операцией в целом. Обозначим его буквой х, а шаговые управления- буквами х1, х2, ... , хm: х=х(х1, х2, ... , хm). Требуется найти такое управление х, при котором выигрыш Z обращается в максимум:
То управление х*, при котором этот максимум достигается, называется оптимальным управлением. Оно состоит из совокупности оптимальных шаговых управлений: х*=х*(х1*, х2*, ... , хm*).
Максимальный выигрыш, который достигается при этом управлении, обозначим следующим образом: ![]() ,
,
где Х- множество допустимых (возможных) управлений.
Самый простой способ решения задачи- полный перебор всех вариантов. Когда количество вариантов невелико, этот способ вполне приемлем. Однако на практике задачи с небольшим числом вариантов встречаются весьма редко, поэтому полный перебор, как правило, неприемлем из-за чрезмерных затрат вычислительных ресурсов. Поэтому в таких случаях на помощь приходит динамическое программирование.
Динамическое программирование часто помогает решить задачу, переборный алгоритм для которой потребовал бы очень много времени. Этот метод использует идею пошаговой оптимизации. В этой идее есть принципиальная тонкость: каждый шаг оптимизируется не сам по себе, а с "оглядкой на будущее", на последствия принимаемого "шагового" решения. Оно должно обеспечить максимальный выигрыш не на данном конкретном шаге, а на всей совокупности шагов, входящих в операцию.
Метод динамического програмирования может применяться только для определенного класса задач. Эти задачи должны удовлетворять таким требованиям:
- Задача оптимизации интерпретируется как n-шаговый процесс управления.
- Целевая функция равна сумме целевых функций каждого шага.
- Выбор управления на k-м шаге зависит только о состояния системы к этому шаге, не влияет на предшествующие шаги (нет обратной связи).
- Состояние sk после k-го шага управления зависит только от предшествующего состояния sk-1и управления xk (отсутствие последействия).
- На каждом шаге управление Xk зависит от конечного числа управляющих переменных, а состояние sk- от конечного числа параметров.
Каково бы ни было состояние системы S в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Этот принцип впервые был сформулирован Р. Беллманом в 1953 г. Беллманом четко были сформулированы и условия, при которых принцип верен. Основное требование- процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.
Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом.
Назначение сервиса . Данный сервис предназначен для решения задачи оптимального распределения инвестиций в онлайн режиме. Результаты вычислений оформляются в отчете формата Word (см. пример оформления).Такого рода задачи основаны на функции Беллмана и при решении используется метод обратной прогонки (см. Типовые задания). Также можно воспользоваться сервисом Процедура прямой прогонки .
Инструкция . Выберите количество предприятий и количество строк (количество вариантов эффективного вложения), нажмите Далее (см. Пример заполнения). Если доход и остатки предприятий задан в виде функций f(x) и g(x) , задача решается через этот калькулятор .
Пример №1 . Определите оптимальный план расширения производства трех предприятий, если известна их прибыль в год при отсутствии вложений и при инвестировании 1, 2, 3 или 4 млн. Определите, при каком инвестировании будет максимальный процент прироста прибыли.
| f1 | f2 | f3 | x i |
| 40 | 30 | 35 | 0 |
| 90 | 110 | 95 | 1 |
| 395 | 385 | 270 | 2 |
| 440 | 470 | 630 | 3 |
| 620 | 740 | 700 | 4 |
I этап. Условная оптимизация
.
1-ый шаг. k = 3.
| e 2 | u 3 | e 3 = e 2 - u 3 | f 3 (u 3) | F* 3 (e 3) | u 3 (e 3) |
| 1 | 0 | 1 | 35 | ||
| 1 | 0 | 95 | 95 | 1 | |
| 2 | 0 | 2 | 35 | ||
| 1 | 1 | 95 | |||
| 2 | 0 | 270 | 270 | 2 | |
| 3 | 0 | 3 | 35 | ||
| 1 | 2 | 95 | |||
| 2 | 1 | 270 | |||
| 3 | 0 | 630 | 630 | 3 | |
| 4 | 0 | 4 | 35 | ||
| 1 | 3 | 95 | |||
| 2 | 2 | 270 | |||
| 3 | 1 | 630 | |||
| 4 | 0 | 700 | 700 | 4 |
2-ый шаг. k = 2.
| e 1 | u 2 | e 2 = e 1 - u 2 | f 2 (u 2) | F* 2 (e 1) | F 1 (u 2 ,e 1) | F* 2 (e 2) | u 2 (e 2) |
| 1 | 0 | 1 | 30 | 95 | 125 | 125 | 0 |
| 1 | 0 | 110 | 0 | 110 | |||
| 2 | 0 | 2 | 30 | 270 | 300 | ||
| 1 | 1 | 110 | 95 | 205 | |||
| 2 | 0 | 385 | 0 | 385 | 385 | 2 | |
| 3 | 0 | 3 | 30 | 630 | 660 | 660 | 0 |
| 1 | 2 | 110 | 270 | 380 | |||
| 2 | 1 | 385 | 95 | 480 | |||
| 3 | 0 | 470 | 0 | 470 | |||
| 4 | 0 | 4 | 30 | 700 | 730 | ||
| 1 | 3 | 110 | 630 | 740 | 740 | 1 | |
| 2 | 2 | 385 | 270 | 655 | |||
| 3 | 1 | 470 | 95 | 565 | |||
| 4 | 0 | 740 | 0 | 740 |
3-ый шаг. k = 1.
| e 0 | u 1 | e 1 = e 0 - u 1 | f 1 (u 1) | F* 1 (e 0) | F 0 (u 1 ,e 0) | F* 1 (e 1) | u 1 (e 1) |
| 1 | 0 | 1 | 40 | 125 | 165 | 165 | 0 |
| 1 | 0 | 90 | 0 | 90 | |||
| 2 | 0 | 2 | 40 | 385 | 425 | 425 | 0 |
| 1 | 1 | 90 | 125 | 215 | |||
| 2 | 0 | 395 | 0 | 395 | |||
| 3 | 0 | 3 | 40 | 660 | 700 | 700 | 0 |
| 1 | 2 | 90 | 385 | 475 | |||
| 2 | 1 | 395 | 125 | 520 | |||
| 3 | 0 | 440 | 0 | 440 | |||
| 4 | 0 | 4 | 40 | 740 | 780 | 780 | 0 |
| 1 | 3 | 90 | 660 | 750 | |||
| 2 | 2 | 395 | 385 | 780 | |||
| 3 | 1 | 440 | 125 | 565 | |||
| 4 | 0 | 620 | 0 | 620 |
Примечание : Столбцы 1 (вложенные средства), 2 (проект) и 3 (остаток средств) для всех трех таблиц одинаковы, поэтому их можно было бы сделать общими. Столбец 4 заполняется на основе исходных данных о функциях дохода, значения в столбце 5 берутся из столбца 7 предыдущей таблицы, столбец 6 заполняется суммой значений столбцов 4 и 5 (в таблице 3-го шага столбцы 5 и 6 отсутствуют).
В столбце 7 записывается максимальное значение предыдущего столбца для фиксированного начального состояния, и в 8 столбце записывается управление из 2 столбца, на котором достигается максимум в 7.
Этап II. Безусловная оптимизация .
Из таблицы 3-го шага имеем F* 1 (e 0 = 4 млн.руб.) = 780 тыс.руб., то есть максимальная прибыль от инвестирования e 0 = 4 млн.руб. равна 780 тыс.руб.
Из этой же таблицы получаем, что первому предприятию следует выделить u* 1 (e 0 = 4 млн.руб.) = 0 млн.руб.
При этом остаток средств составит: e 1 = e 0 - u 1 , e 1 = 4 - 0 = 4 млн.руб.
Из таблицы 2-го шага имеем F* 2 (e 1 = 4 млн.руб.) = 740 тыс.руб., т.е. максимальная прибыль при e 1 = 4 млн.руб. равна 740 тыс.руб.
Из этой же таблицы получаем, что второму предприятию следует выделить u* 2 (e 1 = 4 млн.руб.) = 1 млн.руб.
При этом остаток средств составит: e 2 = e 1 - u 2 , e 2 = 4 - 1 = 3 млн.руб.
Последнему предприятию достается 3 млн.руб. Итак, инвестиции в размере 4 млн.руб. необходимо распределить следующим образом: первому предприятию ничего не выделять, второму предприятию выделить 1 млн.руб., третьему предприятию выделить 3 млн.руб., что обеспечит максимальную прибыль, равную 780 тыс.руб.
Пример №2 . Имеются 4 предприятия, между которыми необходимо распределить 100 тыс. усл. ед. средств. Значения прироста выпуска продукции на предприятии в зависимости от выделенных средств Х представлены в таблице. Составить оптимальный план распределения средств, позволяющий максимизировать общий прирост выпуска продукции.
Динамическое программирование (ДП) - метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми. Начало развития ДП относится к 50-м годам XX в. Оно связано с именем Р.Беллмана.
Если модели линейного программирования можно использовать в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели ДП применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т. п.
В реально функционирующих больших экономических системах еженедельно требуется принимать микроэкономические решения. Модели ДП ценны тем, что позволяют на основе стандартного подхода с использованием при минимальном вмешательстве человека принимать такие решения. И если каждое взятое в отдельности такое решение малосущественно, то в совокупности эти решения могут оказать большое влияние на прибыль.
Рассматривается управляемый процесс, например, экономический процесс распределения средств между предприятиями, использования ресурсов в течение ряда лет, замены оборудования, пополнения запасов и т. п.
В результате управления система (объект управления) S переводится из начального состояния (So), в конечное состояние (Sn). Предположим, что управление можно разбить на n-шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему S из начального состояния в конечное, представляет собой n-шаговый процесс управления.
На каждом шаге применяется некоторое управленческое решение x k , при этом множество х-{х1,х2,...,хn) называется управлением. Метод динамического программирования опирается на условие отсутствия последействия и условие аддитивности целевой функции.
Условие отсутствия последействия . Состояние S k , в которое перешла система за один K- ый шаг, зависит только от состояния S k -1 и выбранного управления x k , и не зависит от того, каким образом система пришла в состояние Sk 1:
S k (Sk 1, xk )
Также учитывается, что выбор управления на k-ом шаге зависит только от состояния системы к этому шагу:
x k (S k -1 )
На каждом шаге управления x k зависит от конечного числа управляющих переменных. Состояние системы на каждом шаге зависит от конечного числа параметров.
Принцип оптимальности. Каково бы ни было состояние s системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. Основное требование, при котором принцип верен - процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.
Таким образом, решение на каждом шаге оказывается наилучшим с точки зрения управления в целом.
Рекуррентные соотношения Беллмана.
Нахождение оптимального решения управляемого процесса можно произвести на основе рекуррентных соотношений Беллмана. Пусть f k (S k -1 ,x k) - показатель эффективности k – ого шага при всевозможных управлениях . Выделяют обратную и прямую схемы Беллмана.
Таблица 6 . Значения прибыли предприятий
|
Объем выделенных ресурсов |
Прибыль от проектов |
||||
В данной таблице 6. представлены значения прибыли (F;(Q)),которые были получены путем решения производственно-экономической задачи каждого инвестируемого предприятия. Эти значения изменяются в зависимости от объемов вложенных инвестиции.
Таблица 7. Данные о дополнительном доходе предприятий
|
Выделяемые ресурсы | |||||
В данной таблице 7. представлены данные о дополнительном доходе, которое предприятие-инвестор получит от каждого инвестируемого предприятия в зависимости от объема вложенных инвестиций.
В таблице 8. рассчитаны показатели эффективности (Zi(Q)) инвестируемых предприятий, которые были получены с помощью прямой схемы Беллмана.
Таблица 8.Показатели эффективности
|
Выделяемые ресурсы |
Дополнительный доход от проектов |
||||
Рассмотрим нахождение каждого из показателей эффективности:
Для показателей эффективности одного предприятия Zi(0) = pi(0)=0
Z1(200’000)= p1(200"000)=7068135,2
Z1(400"000)= p1(400"000)=2567391,9
Z1(600"000)=p1(600"000)=2216151,6
Z1(800"000)=p1(800"000)=1222330,8
Z1(l"OOO"OOO)= p1(l"000"000)=122233,09 Для показателей эффективности двух предприятий .
Z 2 (0)=p 2 (0)=0
Z 2 (200"000)= max{0 + 70 68135,2; 94 07519,6 + 0 )=9407519,6
Z 2 (400"000)= max{0 + 25 67391,9; 94 07519,6 + 70 68135,2 ; 80 92519,9 + 0}=16475654,8
Z 2 (600"000)=max{0 + 22 16151,6; 94 07519,6 +25 67391,9 ; 80 92519,9 +70 68135,2 ; 80 92353,6 + 0)=15160655,1
Z 2 (800"000)= max{0 + 12 2233,08; 94 07519,6 + 22 16151,6; 80 92519,9 + 25 67391,9; 80 92353,6 + 70 68135,2 : 80 92353,6 + 0}=15160488,8
Z 2 (l"000"000)=max{0 + 12 22330,9; 94 07519,6 + 12 22330,8; 80 92519,9 +22 16151,6; 80 92353,6 + 25 67391,9; 80 92353,6 + 70 68135,2 ; 67 38741,6 + 0}=15160488,8
Для показателей эффективности трех предприятий .
Z 3 (0)= p 3 (0)=0
Z 3 (200"000)= max (0 + 94 07519,6; 507 43194,2 + 0 )=50743194,2
Z 3 (400"000)= max {0 + 8092519,9; 507 43194,2 + 94 07519,6 ; 272 10300,4 + 0}=60150713,8
Z 3 (600"000)= max {0 + 8092353,6; 507 43194,2 + 8092519,9 ; 272 10300,4+94 07519,6; 272 10300,4 + 0}=58835714,1
Z 3 (800"000)= max {0 + 8092353,6:507 43194,2 + 8092353,6 ; 272 10300,4 +9407519,6; 272 10300,4 + 8092519,9; 272 10300,5 + 0}= 58835547,8
Z 3 (l "000"000)= max {0+6738741,6; 507 43194,2 + 8092353,6 ; 272 10300,4 + 8092353,6; 272 10300,4 + 8092519,9; 272 10300,5 + 94 07519,6; 27210300,4+0}=58835547,8
Для показателей эффективности четырех предприятий .
Z 4 (0)=p 4 (0)=0
Z 4 (200"000)= max (0 + 507 43194,2 ; 118 73132,7 + 0}= 507 43194,2
Z 4 (400"000)= max {0 + 27210300,4; 118 73132,7 + 507 43194,2 ; 84 75336,3+0}=62616326,9
Z 4 (600"000)= max {0 + 27210300,4; 118 73132,7 + 27210300,4; 84 75336,3 + 507 43194,2 ; 84 75336,3 + 0}= 59218530,5
Z 4 (800"000)= max {0 + 27 210 300,5; 11 873 132,7 + 27 210 300,4; 8 475 336,3+27 210 300,4; 8 475 336,3 + 50 743 194,2 ; 71 37734,9 + 0}=59218530,5
Z 4 (l "000"000)= max {0 + 27210300,4; 118 73132,7 + 27210300,5; 84 75336,3+ 27210300,4; 84 75336,3 + 27210300,4; 71 37734,9 + 507 43194,2 ; 62 83185,8+0}=57880929,1
Для показателей эффективности пяти предприятий .
Z 5 (0)=p 5 (0)=0
Z 5 (200"000)= max (0 + 11873132,7 ; 103 07000,5 + 0}= 11873132,7
Z 5 (400"000)= max (0 + 8475336,3; 103 07000,5 + 11873132 ,7; 77 36093,1+ 0}=22180133,2
Z 5 (600"000)= max (0 + 8 475 336,3; 10 307 000,5 + 8 475 336,3; 7 736 093,1+11 873 132,7 ; 7 736 093,2 + 0}=19609225,8
Z 5 (800"000)= max {0 + 7137734,9; 10 307000,5 + 8 475336,3; 77 36093,1 + 8475336,3; 77 36093,2 + 11873132,7 ; 72 41299,8 + 0}= 19609225,9
Z 5 (l "000000)= max {0 + 6283185,8; 103 07000,5 + 7137734,9; 77 36093,1 + 8475336,3;7736093,2+ 8475336,3; 72 41299,8+11873132,7 ; 71 67372,4+, 0}=19714432,5
После получения последнего показателя эффективности можно получить решение задачи:
Z 5 (1"000"000)= 103 07000,5 + 59218530,5 = 69525531,00 Q 1 = 20 000 000p.
Z 4 (800"000)= 118 73132,7 + 58835714,1 = 70708846,80 Q 2 = 20 000 000p.
Z 3 (600"000)= 507 43194,2 + 16475654,8 = 67218849,00 Q 3 = 20 000 000 p.
Z 2 (400"000)= 94 07519,6 + 7068135,2 = 164756548 Q 4 = 20 000 000p.
Z1(200000) = p!(200"000)= 70 68135,2 Q 5 = 20 000 000р.
Для получения максимальной прибыли предприятием- инвестором выделенные ресурсы (денежные средства в размере 100 000 000 рублей) должны быть распределены следующим образом - каждому инвестируемому предприятию следует выделить по 20 000 000 рублей. При этом максимальный объединенный показатель эффективности будет равен 70 708 846,80 рублей.
Глава 3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Основные понятия и постановка задачи
В задачах линейного и нелинейного программирования рассматриваются статистические задачи экономики, которые не зависят от времени. Для них оптимальное решение находится за один шаг (этап). Такие задачи называются одноэтапными или одношаговыми. В отличие от них задачи динамического программирования являются многоэтапными или многошаговыми. Многошаговым называют процесс экономики, развивающийся во времени или распадающийся на ряд шагов или этапов.
Особенность метода динамического программирования состоит в том, что управленческое решение состоит из комплекса взаимосвязанных решений. Последовательность взаимосвязанных решений, принимаемых на каждом этапе развития процесса во времени, называют стратегией или управлением. В экономике управление сводится к распределению и перераспределению средств (ресурсов) на каждом этапе.
Рассмотрим некоторый развивающийся экономический процесс, разделяющийся по времени из нескольких этапов (шагов). На каждом шаге выбираются параметры, влияющие на ход и исход операции, и принимается решение, от которого зависит выигрыш и на данном шаге по времени, например, в текущем году, и в операции в целом, например, за пятилетку. Этот выигрыш называется шаговым управлением.
Управление процессом в целом распадается на совокупность шаговых управлений : ![]() . В общем случае – числа, векторы, функции. Нужно найти такое управление , при котором выигрыш (например, доход) является максимальным
. В общем случае – числа, векторы, функции. Нужно найти такое управление , при котором выигрыш (например, доход) является максимальным  . Управление , при котором этот максимум достигается, называется оптимальным и состоит из шаговых управлений
. Управление , при котором этот максимум достигается, называется оптимальным и состоит из шаговых управлений ![]() . Максимальный выигрыш обозначим .
. Максимальный выигрыш обозначим .
Задачи математического программирования, которые можно представить как многошаговый (многоэтапный) процесс, составляют предмет динамического программирования. При решении задач оптимизации методом динамического программирования нужно на каждом шаге учитывать последствия, к которым приведет в будущем решение, принимаемое в данный момент. Такой способ выбора решения является определяющим в динамическом программировании. Он называется принципом оптимальности.
Метод динамического программирования рассмотрим на отдельных примерах.
1. Задача управления производством. Планируется работа промышленного объединения, состоящего из предприятий, , на период времени из лет, . В начальный период на развитие объединения выделяются средства в размере . Их нужно распределить между предприятиями. В процессе работы выделенные средства частично расходуются. Каждое предприятие за год дает прибыль, зависящую от вложенных в него средств. В начале каждого года средства можно перераспределять. Нужно так распределить средства между предприятиями, чтобы суммарная прибыль объединения за период T летбыла максимальной.
Принятие решения разбивается на шагов, . Управление заключается в начальном распределении и последующих перераспределениях средств. Управление на каждом шаге t
выражается вектором ![]() , где
, где ![]() – объем средств, выделенных i
-му предприятию в начале года t
. Управление процессом в целом состоит из совокупности шаговых управлений
– объем средств, выделенных i
-му предприятию в начале года t
. Управление процессом в целом состоит из совокупности шаговых управлений ![]() .
.
Пусть – материальное и финансовое состояние системы на начало t
-го года, ![]() . Состояние каждого предприятия также является вектором. Его компонентами являются трудовые ресурсы, основные фонды, финансовое положение и т.д. То есть
. Состояние каждого предприятия также является вектором. Его компонентами являются трудовые ресурсы, основные фонды, финансовое положение и т.д. То есть ![]() , где – число компонент вектора. Вектор управления – это функция состояния системы предприятий на начало соответствующего финансового года . Начальное состояние системы задается.
, где – число компонент вектора. Вектор управления – это функция состояния системы предприятий на начало соответствующего финансового года . Начальное состояние системы задается.
Целевая функция – суммарная прибыль объединения за лет. Пусть – прибыль объединения за год . Тогда целевая функция  . На состояние системы и вектор управления в каждом году могут быть наложены ограничения. Пусть – множество этих ограничений, которое называется множеством допустимых управлений или множеством экономических возможностей. Возможные управления должны принадлежать ей . Таким образом, окончательно задача имеет вид
. На состояние системы и вектор управления в каждом году могут быть наложены ограничения. Пусть – множество этих ограничений, которое называется множеством допустимых управлений или множеством экономических возможностей. Возможные управления должны принадлежать ей . Таким образом, окончательно задача имеет вид  .
.
2. Задача о ремонте и замене оборудования . Владелец автомашины эксплуатирует её в течение m лет. В начале каждого года он может принять одно из трёх решений: 1) продать машину и заменить её новой; 2) отремонтировать и продолжать эксплуатацию; 3) продолжить эксплуатацию без ремонта.
Пошаговое управление – выбор одного из трех решений. Его нельзя выразить числами, но можно приписать первому значение 1, второму – 2, третьему – 3. Как чередовать управления 1, 2, 3 по годам, чтобы суммарные расходы на ремонт, эксплуатацию, покупку новой машины были минимальными:  .
.
Управление операций представляет собой какую-то комбинацию чисел, например: . Любое управление – это вектор такого вида, содержащий m компонент, каждый из которых принимает одно из трех значений 1, 2, 3.
Особенности задач динамического программирования.
1. В этих задачах вместо поиска оптимального решения сразу для всей сложной задачи переходят к нахождению оптимального решение для нескольких более простых задач аналогичного содержания, на которые распадается исходная задача.
2. Решение, принимаемое на конкретном шаге, не зависит от «предыстории»: от того, каким образом оптимизируемый процесс достиг настоящего состояния. Оптимальное решение выбирается с учетом факторов, характеризующих процесс в данный момент;
3. Выбор оптимального решения на каждом шаге по времени производится с учетом его последствий. Оптимизируя процесс на каждом отдельном шаге, нельзя забывать обо всех последующих шагах.
Общая постановка задачи динамического программирования.
Рассмотрим некоторую развивающуюся во времени систему управления, на которую можно влиять принимаемыми решениями. Пусть эта система распадается на T шагов (этапов). Ее состояние на начало каждого шага описывается вектором ![]() . Множество всех состояний, в которых может находиться система на начало t
-го шага, обозначим через . Начальное состояние системы считается известным, то есть при задан вектор .
. Множество всех состояний, в которых может находиться система на начало t
-го шага, обозначим через . Начальное состояние системы считается известным, то есть при задан вектор .
Развитие системы состоит в последовательном переходе из одного состояния в другое. Если система находится в состоянии , то ее состояние на следующем шаге определяется не только вектором , но и управленческим решением , принятым на шаге t
. Запишем это следующим образом . Решение на каждом шаге нужно выбирать из некоторого множества возможных решений, оно не может быть произвольным. Развитие системы в течение всего рассматриваемого периода можно описать последовательностью состояний ![]() , где .
, где .
Любая последовательность допустимых решений, переводящая систему из начального состояния в конечное состояние , называют стратегией. Для полного описания процесса, состоящего из шагов, каждой стратегии надо дать оценку – значение целевой функции , которая представима в виде суммы оценочных функций , значения которых находятся на каждом шаге при переходе из состояния в состояние , т.е.  .
.
Общую задачу динамического программирования можно сформулировать так. Найти стратегию , доставляющую экстремум функции  при условиях, что задан вектор начального состояния системы , а вектор текущего состояния системы на момент времени является функцией состояния системы на момент времени и управленческого решения, принятого на этом шаге: , .
при условиях, что задан вектор начального состояния системы , а вектор текущего состояния системы на момент времени является функцией состояния системы на момент времени и управленческого решения, принятого на этом шаге: , .
Функциональные уравнения динамического программирования называются функциональными уравнениями Беллмана .
Математическая формулировка принципа оптимальности с аддитивным критерием . Пусть заданы начальное и конечное состояние системы . Введем обозначения: – значение функции цели на первом этапе при начальном состоянии системы X 0 и при управлении , – значение функции цели на втором шаге при состоянии системы и при управлении . Соответственно далее – значение функции цели на -ом этапе, . Очевидно, что
Требуется найти оптимальное управление ![]() , такое что
, такое что
при ограничениях
Поиск оптимального решения задачи (69)–(70) сводится к оптимальному решению нескольких более простых задач аналогичного содержания, которые входят составной частью в исходную задачу.
Пусть – соответственно области определения (допустимых решений) для задачи на последнем этапе, на последних двух этапах и т.д., – область определения исходной задачи. Пусть – условно оптимальное значение функции цели на последнем этапе, т.е.
![]() , . (71)
, . (71)
Обозначим соответственно оптимальные значения функции цели на двух последних, трех последних этапах и т.д., на Т этапах. В силу этих обозначений имеем:
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
Выражения (71) – (75) называются функциональными уравнениями Беллмана. Эти уравнения имеют рекуррентный характер, так как для нахождения оптимального уравнения на T шагах нужно знать условно оптимальное управление на последующих T –1 шагах и т.д. Поэтому функциональные уравнения также называют рекуррентными соотношениями Беллмана.
Используя функциональные уравнения Беллмана, находим решение рассматриваемой задачи динамического программирования. Решение ищется в обратном порядке от до .
Запишем функциональное уравнение последнего этапа
![]() .
.
Рассматривают набор фиксированных состояний и решений и отвечающих им значений . Среди решений выбирают такое , которое обеспечивает максимум (минимум) функции . Затем переходят к предшествующему этапу и рассматривают функциональное уравнение (72). Для каждого возможного состояния находят значение в зависимости от допустимого решения . Затем сравнивают суммы и определяют максимальную (минимальную) сумму для каждого состояния и соответствующее условное оптимальное решение , т.е. определяют решение, при котором функция принимает экстремальное значение.
Далее переходят к этапам ( и т.д.) до момента времени . Для первого этапа записывают функциональное уравнение (75). На этом шаге предположения о возможных состояниях процесса не делают, так как первоначальное состояние известно. Для этого состояния находится оптимальное решение с учетом всех условно оптимальных решений предыдущих этапов.
Весь процесс проходят в прямом направлении от до и определяют оптимальное решение для всего процесса (всей задачи). Оно придает целевой функции максимальное (минимальное) значение.
Задача выбора кратчайшего пути . Задана транспортная железнодорожная сеть (рис.11), на которой указан пункт отправления A и пункт назначения B. Между ними имеется много других пунктов. Некоторые соединены между собой железнодорожным полотном. Над каждым участком железнодорожной сети проставлены цифры, указывающие расстояние между двумя соседними пунктами. Требуется составить маршрут из пункта A в пункт B минимальной длины.
Разобьем все расстояние между A и B на этапы (рис.11). Оценим отрезки, на которые делят линии (2-2) и (3-3) участки сети.

Выбор кратчайшего пути начнем с конца. Найдем кратчайшие пути, соединяющие конечный пункт B с каждой точкой пересечения линии (2-2) с транспортной сетью. Таких точек пересечения три: D 1 , D 2 , D 3 . Для точки D 1 min(10;8+4;8+3+5)=10; для точки D 2 min(5+4;5+3+5)=9; для точки D 3 min(2.5+3+4; 2.5+5)=7.5.
На рисунке кратчайшие расстояния от точек D 1 ,D 2 и D 3 до конечного пункта B показаны в скобках. Далее рассматриваем точки пересечения линии (3-3) с участком сети. Эти точки C 1 , C 2 , C 3 . Находим кратчайшие расстояния от этих точек до пункта B. Они показаны в скобках у точек C 1 (19), C 2 (14), C 3 (12). Наконец находим минимальную длину пути, ведущего из A в B. Это расстояние равно 23. Затем находим этапы в обратном порядке. Находим кратчайший путь: ![]() .
.
Ключевые слова : динамическое программирование, многоэтапный процесс, управление, управляемый процесс, стратегия, оптимальная стратегия, принцип оптимальности, условно оптимальное управление, функциональные уравнения Беллмана.
Вопросы для самопроверки
1. Что является предметом динамического программирования?
2. В чем отличие динамического программирования от линейного программирования?
3. Каковы основные свойства динамического программирования?
4. В чем заключается принцип оптимальности динамического программирования?
5. Какова модель задачи планирования работы промышленного объединения?
6. Какова формулировка общей задачи динамического программирования?
7. Что выражают функциональные уравнения Беллмана?
8. В чем заключается идея решения задачи динамического программирования?
Задачи для самостоятельного решения
Пример 1. Сформулировать приведенные задачи в терминах динамического программирования.
А) Производственное объединение состоит из т предприятий. В начале каждого года между ними полностью распределяется централизованный фонд развития производства. Выделение i -му предприятию из этого фонда тыс.руб. обеспечивает получение дополнительной прибыли, равной тыс. руб. К началу планового периода из T лет централизованному фонду развития производства выделено тыс.руб. В каждый последующий год этот фонд формируется за счет отчислений от полученной прибыли. Эти отчисления для i -го предприятия составили тыс.руб. Найти такой вариант распределения централизованного фонда развития производства, чтобы получить за T лет максимальную общую прибыль.
Б) В состав производственного объединения входят два предприятия, связанные между собой кооперированными поставками. Вкладывая дополнительные средства в их развитие, можно улучшить технико-экономические показатели деятельности производственного объединения в целом, обеспечив получение дополнительной прибыли. Ее величина зависит от величины средств, выделяемых каждому предприятию, и использованию этих средств. Считая, что на развитие i -го предприятия в начале k -го года выделяется тыс.руб., найти такой вариант распределения средств между предприятиями в течении T лет, чтобы за данный период времени будет получить максимальную прибыль.
Пример 2. Требуется перевезти груз из пункта A в пункт B.

На рис.12 показана сеть дорог и стоимость перевозки единицы груза между отдельными пунктами сети (проставлены у соответствующих ребер). Определить маршрут доставки груза из пункта A в пункт B, которому соответствуют наименьшие затраты.
Пример 3. На данной сети дорог имеется несколько маршрутов по доставке груза из пункта A в пункт B (рис.13). Стоимость перевозки единицы груза между отдельными пунктами сети проставлена у соответствующих ребер. Определить оптимальный маршрут доставки груза из пункта A в пункт B, по которому общие затраты будут минимальными.

Задача распределения инвестиций между предприятиями
На реконструкцию и модернизацию основного производства объединению выделяются материальные ресурсы в объеме . Эти ресурсы нужно распределить между n предприятиями объединения.
Пусть – прибыль, получаемая, если i -му предприятию выделено единиц ресурса. Общая прибыль объединения складывается из прибылей отдельных предприятий
Математическая модель распределения инвестиций имеет вид
Требуется добиться максимума целевой функции (76) при условиях полного распределения инвестиций объема между предприятиями (77) и неотрицательности переменных (78).
Решение задачи представим в виде многоэтапного процесса. Вместо решения одной задачи с заданным объемом инвестиций и фиксированным числом предприятий n рассмотрим семейства задач, в которых объем выделяемого ресурса может меняться от 0 до , а число предприятий – от 1 до n . Например, предполагается, что на первом этапе инвестиция в объеме выделяется только одному предприятию, на втором этапе – двум предприятиями и т.д., на n -ом этапе – предприятиям.
Введем последовательность функций , где – максимальное значение прибыли, получаемой, когда ресурс x
распределен только одному предприятию; – максимальное значение прибыли, получаемой при условии, что объем ресурса распределен между двумя предприятиями и т.д.; – максимальное значение прибыли, получаемой при условии, что ресурс распределен между n
предприятиями. Очевидно, что ![]() .
.
В двух случаях элементы последовательности имеют простой вид: . Эти соотношения означают: если инвестиция не распределяется, то ожидаемая прибыль равна нулю, и если инвестиция распределяется одному предприятию, то прибыль объединения будет состоять из прибыли только одного предприятия.
Пусть инвестиция объема x , , распределяется между двумя предприятиями. Если – объем инвестиций, выделенный второму предприятию, то его прибыль составит
![]() .
.
Допустим, что инвестиция объема x распределяется между k предприятиями. Если – объем инвестиций, выделенный k -му предприятию, то оставшееся количество ресурса распределяется между оставшимися k –1 предприятиями наилучшим образом. Так как известно, то
![]() . (79)
. (79)
Полученное рекуррентное соотношение (79) и есть функциональное уравнение Беллмана.
Решение исходной задачи получим при из соотношения (79):
Рассмотрим вычислительную схему решения задачи распределения инвестиций методом динамического программирования.
Промежуток разбивают, например, на N интервалов с шагом и считают, что функции определены для значений . При i =1 функция определяется равенством . Множество значений , записывают в таблицу. Зная значения , переходят к вычислению значений функции :
В ходе вычислений устанавливают не только значения ![]() , но и такие значения , при которых достигается максимум прибыли . Затем находят значения функции и т.д. Пройдя весь процесс вычисления функций , получают соотошение
, но и такие значения , при которых достигается максимум прибыли . Затем находят значения функции и т.д. Пройдя весь процесс вычисления функций , получают соотошение
с помощью которого находят значение ![]() . Таким образом, на последнем этапе находят максимальное значение функции цели , а также оптимальное значение выделяемого ресурса для n
-го предприятия.
. Таким образом, на последнем этапе находят максимальное значение функции цели , а также оптимальное значение выделяемого ресурса для n
-го предприятия.
Затем процесс вычислений просматривается в обратном порядке. Зная , находят – объем инвестиций, подлежащий распределению между оставшимися n– 1 предприятиями.
Прежде всего, используя соотношение
находят значения и и т.д. Продолжая таким образом, в конце процесса находится значение .
Пример 1. Между четырьмя предприятиями следует распределить 200 единиц ограниченного ресурса. Значения, получаемой предприятиями прибыли в зависимости от выделенной суммы , приведены в табл.57 , составленной с «шагом» единиц ресурса. Составить план распределения ресурса, дающий наибольшую суммарную прибыль.
Таблица 57
| Выделяемый объем инвестиций | Величина прибыли предприятия | |||
Решение. Представим поставленную задачу как четырехэтапную. На первом этапе, при , рассмотрим случай, когда инвестиция выделяется только одному предприятию. В этом случае . Для каждого значения из промежутка находим значения и заносим их в таблицу 58.
Таблица 58
При инвестиция распределяется между двумя предприятиями. В этом случае общая прибыль вычисляется с помощью следующего функционального уравнения
![]() . (80)
. (80)
· пусть , то :
· пусть , то ![]() :
:

· пусть то :

· пусть , то :

Результат вычисления запишем в табл.59.
Таблица 59
| 0+15 | 14+0 | |||||||
| 0+28 | 14+15 | 30+0 | ||||||
| 0+60 | 14+28 | 30+15 | 55+0 | |||||
| 0+75 | 14+60 | 30+28 | 55+15 | 73+0 | ||||
| 0+90 | 14+75 | 30+60 | 55+28 | 73+15 | 85+0 |
На 3-ем этапе инвестиция в объеме единиц распределяется между тремя предприятиями. В этом случае общая прибыль объединения определяется с помощью функционального уравнения
![]() .
.
Результаты вычислений представим в табл.60.
Таблица 60
| 0+15 | 17+0 | |||||||
| 0+30 | 17+15 | 33+0 | ||||||
| 0+60 | 17+30 | 33+15 | 58+0 | |||||
| 0+75 | 17+60 | 33+30 | 58+15 | 73+0 | ||||
| 0+90 | 17+75 | 33+60 | 58+30 | 73+15 | 92+0 |
На 4-м этапе инвестиция распределяется между четырьмя предприятиями и общая прибыль при этом распределяется с помощью функционального уравнения
- Граница между европой и азией Америка относится к европе
- Как экономить деньги при маленькой зарплате?
- Порядок получения жилищной субсидии для военнослужащих
- Лимит кассы: нормативная база и сроки установления лимита
- Полная система вычетов Алгебраическая форма комплексного числа
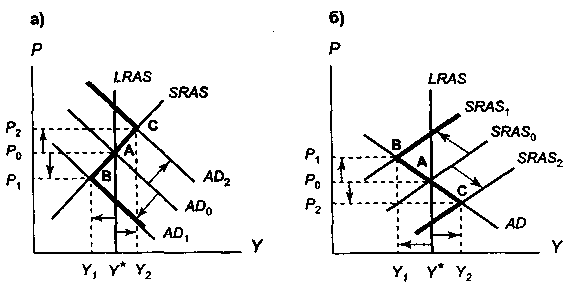
- Модель «Совокупный спрос – совокупное предложение Увеличение совокупного спроса вызывает
- Что называется периодом в физике
- Виды и типы недвижимости, их экономическая составляющая Поля инициализаторов типа
- Экономика, население и города Чеченской Республики
- Особенности проведения региональной программы материнский капитал в московской области Региональный материнский капитал программе семья
- Должностная инструкция страхового агента росгосстрах
- Учет материалов на складе и в бухгалтерии
- На вопрос «Можно ли строить дом без разрешения на строительство?
- Ип на осно какие налоги платит?
- Доходы и расходы будущих периодов Как распределить расходы, затрагивающие несколько налоговых периодов
- Экономические циклы, их особенности и виды
- Необходимо знать от чего зависят цены на жилье
- Контрольная работа: Экономическая мысль Древней Греции
- Бухгалтерские проводки по реализации товаров и услуг 1с бухгалтерия 8
- Оборотные активы организации