Линия тренда в Excel на разных графиках. Общая статистика – лекции (дно)
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:


Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание!!! Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:

На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):

Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).

Получаем результат:

Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:

Строим график. Добавляем экспоненциальную линию.

Уравнение имеет следующий вид:
y = 7,6403е^-0,084x
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:

R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
Например:
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).

Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.

Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ . Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.


Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ . Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ , а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа» , но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.


Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ , так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.


Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ . Его синтаксис имеет такой вид:
ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН , умноженный на количество лет.


Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ . Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.


Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.
Если изучаемый процесс приводит к замедлению роста какого-то показателя, но при этом рост не прекращается, не стремится к какому-либо ограниченному пределу, то гиперболическая форма тренда уже не подходит. Тем более не подходит парабола с отрицательным ускорением, по которой замедляющийся рост перейдет со временем в снижение уровней. В указанном случае тенденция изменения лучше всего отображается логарифмической формой тренда: = a + b ln .
Логарифмы возрастают значительно медленнее, чем сами числа (номера периодов ), но рост логарифмов неограничен. Подбирая начало отсчета периодов (моментов) времени, можно найти такую скорость снижения абсолютных изменений, которая наилучшим образом отвечает фактическому временному ряду.
Примером тенденций, соответствующих логарифмическому тренду, может служить динамика рекордных достижений в спорте.
Основные свойства логарифмического тренда:
1. Если b>0, то уровни возрастают, но с замедлением, а если b<0, то уровни тренда уменьшаются, тоже с замедлением.
2. Абсолютные изменения уровней по модулю всегда уменьшаются со временем.
3. Ускорения абсолютных изменений имеют знак, противоположный самим абсолютным изменениям, а по модулю постепенно уменьшаются.
4. Темпы изменения (цепные) постепенно приближаются к 100% при .
Можно сделать общий вывод о том, что логарифмический тренд отражает, так же как и гиперболический тренд, постепенно затухающий процесс изменений. Различие состоит в том, что затухание по гиперболе происходит быстро при приближении к конечному пределу, а при логарифмическом тренде затухающий процесс продолжается без ограничения гораздо медленнее
Адаптивные методы
Опр . Адаптивными методами прогнозирования (или моделями экспоненциального сглаживания) называется методы, позволяющие строить самокорректирующиеся ЭММ, которые учитывают результат реализации прогноза, сделанного на предыдущем шаге, и строят прогноз с учетом полученных результатов.
Инструментом прогноза в адаптивных методах прогнозирования служат математические модели, изначальная оценка параметров, которых осуществляется обычно по некоторой выборке исходного ряда, называемого обучающей последовательностью.
Алгоритм построения модели адаптивного прогнозирования укладывается в следующую схему:
Для начала делается оценка начальных условий (так называемые нулевые значения адаптируемых параметров), затем делается прогноз на один шаг вперед, полученные прогнозные значения сравниваются с фактическими значениями. Если ошибка прогноза превышает заданной наперед определенной погрешности, то производят модификацию модели, и с учетом этого строят новый прогноз, далее на второй шаг, и опять сравнивают полученный прогноз с фактической реализацией процесса. Процесс повторяют до тех пор, пока разница, между прогнозным и фактическим значениями, не станет минимальной. Таким образом, будут получены параметры адаптируемой модели, и с учетом их значений строят ретроспективный прогноз.
37 . Модель Брауна.
Самой простой моделью адаптивного прогнозирования является модель Брауна, которая выглядит следующим образом:
х с волной(?)=а0т+ а1т* т (1).где - прогноз, выполненный на? шагов вперед на t-м шаге адаптации, - адаптируемые параметры модели, ? – период упреждения. Параметры рассчитываются по формулам:
система:а0т=2St (1) - St (2), f1t=1 -бетта/бетта *(St(1)- St(2)), (2) где - экспоненциальные средние соответственно 1-го и 2-го порядков; ? – параметр сглаживания (адаптации). Иногда параметр сглаживания обозначают как?=1-? Экспоненциальная средняя 1- го порядка представляет собой сумму взвешенных значений переменной за весь предшествующий период адаптации и определяется формулой:St(1)=(1-бетта)*хе + бетта*St-1(1),: (3)
где? – параметр сглаживания, или так называемый весовой коэффициент, - фактическое значение обучающего множества, - экспоненциальная средняя на предшествующем шаге.
Экспоненциальную среднюю можно выразить через предшествующую экспоненциальную среднюю: St-1(1)=(1-бетта)*хе-1 + бетта*St-2(1), (4) подставив (4) в (2) получим:St(1)=(1-бетта)*хе+бетта*(1-бетта)*хt-1+бетта в кв* St-2(1),(5)Аналогично можно выразить через предшествующую экспоненциальную среднюю и подставить в уравнение (3) и, и, и т.д. Отсюда имеем St-2 (1)= (1-бетта)*сумма от 0 до 1 БЕТТА (j)*хt-j+бетта (t)*S0(1).(6) Таким образом, применив такую процедуру экспоненциального сглаживания к исходному ряду, получим сглаженный ряд первого порядка. Повторное применение процедуры экспоненциального сглаживания уже к сглаженному ряду первого порядка, называется процедурой экспоненциального сглаживания второго порядка (к применяем формулу (3)):St(2)=(1- бетта)*St(1)+ бетта*St-1 (2),(7) Начальные значения экспоненциальных средних будут определяться по формулам:система:S0(1)=a00- (бетта/1- бетта) *а10; S0 (2)=a00-(2*бетта/(1-бетта))*а10,(8),Система (8) получена решением системы (2) относительно при t=0.
Начальные значения параметров (необходимы для решения системы (8)) рассчитываются как коэффициенты регрессии хт=а00+а10*т.Отметим, что значение параметра адаптации?=1-? лежит в интервале (1; 0). Выбор значения? зависит от того, каким значениям исходного ряда (начальным или конечным) придается больший вес. Если требуется придать вес более поздним значения ряда (увеличить степень реагирования модели на последние изменения), то берут значения? больше 0,5. Если же хотят получить более сглаженную картину тенденции развития ряда, то есть стремятся избежать краткосрочных изменений и повысить степень устойчивости модели, то значения? берут меньше 0,5, и таким образом придают вес ранним наблюдениям ряда.
Будем рассматривать два способа определения параметра адаптации?:
1) метод Брауна алфа=2/m+1, где m –число наблюдений в ряду.
2) метод выбора?, исходя из минимума средней квадратической ошибки между расчетным и фактическим значениями.
Иногда адаптивную модель Брауна называют моделью линейного роста Брауна.
Модель Хольта.
Модель Хольта, содержащая два параметра адаптации, выглядит следующим образом: х с волной е(р)=ае+бе*р (3.1.),где - прогноз, выполненный на? шагов вперед после t шагов адаптации, - корректируемые параметры модели на каждом шаге t, ? – период упреждения прогноза. Адаптация параметров модели происходят по следующим формулам:система:ае=альфа1*х1+ (1- альфа)*(ае-1+бе-1); бт=альфа2*(фе-фе-1)+(1-фльфа2)*бт-1,(3.2) где? – параметры адаптации.
- Модель Хольта-Уинтерса.
Модель Хольта-Уинтерса имеет другое название адаптивной сезонной модели с линейным трендом имеет три параметра адаптации. Различают аддитивную и мультипликативную модель Хольта-Уинтерса в зависимости от того, как включена сезонная составляющая (умножение или сложение). Рекуррентные формулы для обновления мультипликативной модели:система:а0е=альфа*(хт/фт-1)+(1-альфа1)*(ф0е-1+ф1т-1); а1т=альфа2*(а0т-а0т-1)+(1-альфа2)*ат-1;фе=альфа3*(хт/а0т)+(1-альфа3)*фе-ий
(4.1) где - адаптируемые параметры линейного тренда на t-м шаге адаптации, - параметры адаптации, - адаптируемый параметр сезонных коэффициентов на t- м шаге адаптации, l – период сезонности. Прогнозирование в мультипликативной модели на? шагов вперед осуществляется по формуле:х с фолной т+р=а0т+ф1т*р+фе-1+р, 4.5)Определение начальных параметров а00,а10,фий-1 (i=0, 1, …,l) для параметров адаптации альфа 1 2 3 исходит из следующих требований: параметры а00,а10 определяются как коэффициенты регрессии хт=а00+а10*т, адаптируемые же коэффициенты сезонности определяются как среднее арифметическое значение индексов фс волной т=хт-у расч.т (для мультипликативной модели) и ф с волной=хт-у расч.т.
(для аддитивной модели), причем рассчитываются они для каждой одноименной фазы периода (-расчетные значения линейного тренда).
Параметры альфа 1,2,3 определяются обычно из условия минимизации суммы квадратов ошибок, причем необходимо учитывать, что альфа 2 параметр сглаживания тренда, а - альфа3 параметр адаптации сезонных коэффициентов
Рисунок 7. Экспоненциальный тренд
Экспоненциальный тренд описывает процессы, развивающиеся в условиях отсутствия значимых ограничений изменения уровня. Уровни тренда представляют собой геометрическую прогрессию. Очевидно, что обычно он имеет место на ограниченных отрезках времени.
Основное выражение гиперболического тренда

Рисунок 8. Гиперболический тренд
Свободный член уравнения, таким образом – это предел, к которому стремятся уровни ряда. Такая тенденция характерна для процессов демонстрирующих тенденцию к замедляющемуся снижению значений показателя, которые, однако, не могут уменьшиться более некоторого нижнего значения. Например, такими свойствами могут обладать тенденции снижения затрат на производство . В случае b < 0 с течением времени уровни тренда, наоборот, возрастают, стремясь к а .
Если изучаемый и прогнозируемый процесс приводит к замедлению роста показателя, но не вызывает прекращения роста, то вполне адекватным отображением тенденции может стать уравнение логарифмического тренда:
![]() .
.

Рисунок 9. Логарифмический тренд
Подбирая начало отсчета периодов, можно найти такую скорость изменений, которая наиболее точно отвечает фактическому временному ряду .
Логистическая форма уравнения тренда подходит для описания процесса, когда изучаемый показатель проходит полный цикл развития, начиная от нижнего (как правило, нулевого) уровня, сначала медленно с ускорением возрастая, после чего тенденция становится приблизительно прямолинейной. В завершающей части цикла рост замедляется по гиперболе по мере приближения к пределу. В некоторых зарубежных прикладных пакетах статистического анализа логистическая кривая называется S-образной кривой.
Можно считать логисту объединением сразу трех видов тенденций: парабола – прямая – гипербола. Но есть и доводы за рассмотрение логистического тренда как самостоятельного. Его выделение позволяет уже на первом этапе определить всю траекторию развития явления, выяснить сроки перехода от ускоренного роста к замедленному, что может оказаться весьма важно для прогноза.

Рисунок 10. Логистический тренд
При изменении уровней от нулевого уравнение тренда по логисте имеет вид
 .
.
При а0 > 0 и а1 < 0 с ростом номера периодов времени будет иметь место тенденция роста уровней. Если нужно начать рост почти с нуля, то должно быть а0 ≈ 10 . Чем больше будет модуль а1 , тем быстрее будут возрастать уровни. При а1 < 0 и а2 > 0 имеет место тренд снижения уровней ряда, если нужно начать снижение почти от 1 , то должно быть а0 ≈ –10 . Чем больше будет а1 , тем быстрее будут снижаться уровни.
Если диапазон изменения уровней ограничен не нулем и единицей, а обозначенными исходя из условий ymax и ymin , то формула логистического тренда примет вид

Графическое отображение во многих случаях позволяет приближенно выявить вид тип уравнения, наиболее адекватный тенденции временного ряда. Но при этом следует соблюдать некоторые правила построения графика. Требуется точное соблюдение масштаба как по величине уровней ряда, так и по шкале времени. Время откладывается обычно по оси абсцисс, величины уровней – по оси ординат. По каждой оси следует установить такой масштаб, чтобы ширина графика была примерно в 1,5 раза больше его высоты. Если уровни ряда различаются в десятки, сотни, тысячи раз, ось ординат имеет смысл разместить в логарифмическом представлении, равные отрезки будут означать различие уровней в одинаковое число раз. Тогда изменится и интерпретация графика: при линейном масштабе прямая будет означать прямолинейную тенденцию, при логарифмическом – экспоненту. Нужно соблюдать равенство величин, отображающих время на горизонтальной оси, тут логарифмическая шкала не рекомендуется, это значительно осложнит прочтение графика.
Но графический метод не всегда дает хороший результат. Например, таким путем трудно бывает отличить параболу от экспоненты, логарифмическую кривую от гиперболы и т. д. Хотя специализированные прикладные программные пакеты значительно облегчают анализ, в них нередко встроены средства быстрого расчета и нанесения на график линии тренда в соответствии с различными предположениями о его характере (например, нанесение линии тренда на диаграммы в MS Excel). Кроме того, не всегда вариант уравнения тренда, «лучший» внешне, является лучшим с аналитической и статистической точек зрения. Поэтому имеет смысл использовать и иные методы определения типа уравнения тренда: метод последовательных разностей , МНК (выбор уравнения тенденции, дающего наименьшую сумму квадратов отклонений)…
3.1.3. Особенности прогнозирования на основе трендовых моделей
Трендовое прогнозирование обладает свойств:
Для крупных сложных объектов и систем, обладающих большой инерционностью развития, прогноз по тренду, выявленному на базе изучения предыдущего развития, как правило, вполне реален и надежен;
Выясненные параметры тренда (то есть константы аппроксимирующих тренд выражений) должны быть статистически надежны, что достаточно легко проверить. Если они не надежны, то ненадежен и прогноз;
Срок упреждения прогноза должен быть не более половины периода основания прогноза (лучше – не более трети). То есть, если период основания прогноза, в рамках которого изучалась тенденция явления, составляет, скажем, 30 лет, то возможных период упреждения – 10 – 15 лет максимум.
У прогнозирования на базе временных рядов с помощью выясненной тенденции развития есть некоторые преимущества перед другими методами прогнозирования, есть и недостатки.
Уравнение тренда имеет преимущества перед «обычной» статистической регрессией по потенциальной ширине охвата факторов, влияющих на динамику изучаемого явления. Коэффициент при номере периода в уравнении тренда – это комплексный коэффициент регрессии при всех реальных факторах, влияющих на уровень изменяющегося показателя, которые сами изменяются во времени. «Обычная» регрессия (которая, кстати, составляет основу эконометрических моделей) позволяет учесть только часть факторов, влияние остальных «списывается» на ошибку регрессии.
Второе преимущество состоит в том, что уравнение тренда есть модель динамики процесса, и на ее основании мы прогнозируем динамику, т. е. логическая основа тренда соответствует задаче. Напротив, уравнение многофакторной регрессии – это модель вариации уровня показателя в статической совокупности. Логическая база прогноза по многофакторной регрессии в статике не совсем адекватна задаче прогнозирования.
Последнее, хотя и не очень существенное преимущество прогноза по тренду заключается в том, что для него не требуется большого объема исходной информации о факторах, как для множественной регрессии. Достаточно однородного по характеру тенденции периода, допустим, за 20 – 25 лет.
Но прогноз на основе временного тренда может не давать корректных результатов в случае высокой нестабильности объекта предсказания. Нет возможности проигрывать разные варианты прогноза при разных сочетаниях значений факторов, что обычно делается при прогнозе по регрессионной модели с управляемыми факторами (то есть сделать прогноз действительно вариативным). Кроме того, наилучшие результаты трендовое прогнозирование дает на относительно коротких периодах упреждения (краткосрочный, если по годам – среднесрочный прогноз).
Прогноз производится по такому общему алгоритму:
1. упорядочение прошлых данных;
2. сглаживание временного ряда;
3. выделение тренда;
4. определение уравнения тренда;
5. расчет прогнозного значения;
6. оценка доверительного интервала с заданной вероятностью.
В процессе выяснения тренда показателя может потребоваться учет повторяющихся колебаний в рамках самой основной тенденции, своего рода тренда внутри тренда. В данном случае речь идет о периодической колеблемости неслучайного характера, например, о сезонности. В этом случае трендовую модель имеет смысл дополнить до модели тренда и сезонности.
Такую коррекцию можно провести с помощью индексов сезонности. Сезонность – явление, имеющее обычно ежегодную повторяемость. Для ее определения желательно проанализировать данные по 7-ми – 10-ти периодам, в которых имеет она место. Можно обойтись и меньшим числом периодов (например, лет), но тогда достоверность наличия выявленной закономерности снижается.
Можно рассчитывать индексы сезонности как собой частное от деления отдельных уровней ряда на средний по всему ряду, для которого определяется сезонность, уровень. Например, сезонность в рамках года определима индексами, получаемыми в результате деления месячных уровней на среднемесячное значение уровня ряда за весь год. Умножение на 100 даст величину индекса в процентах.
Возможен и расчет сезонных индексов с использованием весов. Тогда используется несколько иной алгоритм расчетов. Обратимся к примеру расчета квартальной сезонности в течение года на основе помесячных данных за несколько лет:
1. определяются индексы сезонности путем соотнесения эмпирических данных (yi ) с рассчитанными по уравнению тренда (https://pandia.ru/text/78/235/images/image028_9.gif" width="71" height="61">;
2..gif" width="21 height=28" height="28">) для каждого уже укрупненного периода времени – собственно сезона (квартал). Роль весов играют средние значения уровней ряда для годов, рассчитанные ранее, где – индексы сезонности по месяцам:
 .
.
Учет периодической колеблемости может осуществляться и иными способами (например, на основе рядов Фурье).
3.2. Эконометрическое моделирование
3.2.1. Общее понятие эконометрических моделей
Эконометрические модели (в основе которых лежат методы статистики, точнее – регрессионного анализа) из всех формализованных методов прогнозирования используются, возможно, наиболее часто (по крайней мере, за рубежом).
В качестве самостоятельной отрасли знания эконометрика оформилась в начале 30-х годов XX века. Термины «эконометрика» и «эконометрия» стали общеупотребительными благодаря норвежскому экономисту Р. Фришу. Согласно Р. Фришу, эконометрика объединяет «как чистую экономическую теорию , так и статистическую проверку законов чистой экономической теории». Более конкретно: «сущность эконометрики заключается во взаимном переплетении количественной экономической теории и статистических оценок». Отсюда следует, что к числу эконометрических относятся отнюдь не все модели, а лишь такие, которые позволяют проводить статистические операции. Существует не мало моделей и развернутых на их основе «количественных теорий», являющихся экономико-математическими, но вовсе не эконометрическими. Поскольку за каждой переменной эконометрической модели стоит определенный статистический индикатор, с той или иной точностью измеряющий какую-то сторону хозяйственного механизма, расчеты на базе этой модели, как правило, имеют достаточно высокую практическую ценность. Они могут быть использованы при выработке экономической политики государства , рыночной стратегии фирмы и решении других конкретных задач.
Методологическая особенность эконометрики заключается в применении общих гипотез о статистических свойствах экономических параметров и ошибок при их измерении. Полученные при этом результаты могут оказаться нетождественными тому содержанию, которое вкладывается в реальный объект. Поэтому важная задача эконометрики – создание как более универсальных, так и специальных методов для обнаружения наиболее устойчивых характеристик в поведении реальных экономических показателей. Эконометрика разрабатывает методы «подгонки» формальной модели с целью наилучшего имитирования ею поведения моделируемого объекта на основе гипотезы о том, что отклонение модельных параметров от реально наблюдаемых случайны и вероятностные характеристики их известны.
Главным инструментом эконометрики служит эконометрическая модель – модель факторного анализа , параметры которой оцениваются средствами математической статистики. Такая модель выступает в качестве средства анализа и прогнозирования конкретных экономических процессов на основе реальной статистической информации.
Можно выделить два основных класса эконометрических моделей:
1) Регрессионные модели с одним уравнением. В таких моделях зависимая (объясняемая) переменная Y представляется в виде функции , где x 1 , …, хn – независимые (объясняющие) переменные, β1, …, β m – параметры. В зависимости от вида функции f (x , β) модели делятся на линейные и нелинейные . Например, можно исследовать среднедушевой уровень потребления населения как функцию от уровня доходов населения и численности населения, или зависимость заработной платы от возраста, пола, уровня образования, стажа работы и т. п. По математической форме они могут быть схожи с моделями временных рядов, в которых в качестве независимой переменной выступает значение момента времени
Область применения таких моделей, даже линейных, значительно шире, чем моделей временных рядов. Проблемам теории оценивания, верификации (проверки на практике), отбора значимых параметров и другим посвящен огромный объем литературы. Эта тема – стержневая в эконометрике.
2) Системы одновременных уравнений. Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых (кроме независимых переменных) может включать в себя также зависимые переменные из других уравнений системы. В результате имеется набор зависимых переменных, связанных через уравнения системы, решаемые одновременно. Примером может служить модель Уортона, имеющая очень большую размерность (уортоновская квартальная модель американской экономики содержит более 1 тыс. уравнений).
3.2.2. Линейная регрессия. Метод наименьших квадратов (МНК)
С помощью методов регрессионного анализа, основных для эконометрического моделирования, строятся и проверяются модели, характеризующие связь между одной эндогенной (зависимой) переменной и одной или более экзогенными (независимыми) переменными. Независимые переменные называются регрессором.
Направленность связи между переменными определяется путем предварительного обоснования и включается в модель в качестве исходной гипотезы. Задача регрессионного анализа – проверка статистической состоятельности модели, если данная гипотеза верна. Регрессионный анализ не в состоянии «доказать» гипотезу, он может лишь подтвердить ее статистически или отвергнуть.
Рассмотрим методологию построения регрессионных эконометрических моделей на примере моделей из одного уравнения . Модели в виде системы уравнений, обладая своими особенностями (в частности, при определении параметров-коэффициентов модели) также базируются на ней.
В общем виде регрессионное уравнение выглядит так:
![]() ,
,
где – функция, которая описывает детерминированную составляющую модели (само уравнение регрессии), ε представляет собой «случайную» компоненту.
Обычно наиболее часто для отображения зависимости используются линейные регрессионные уравнения, отображающие зависимость в виде прямой в многомерном пространстве. В случае с парной линейной регрессией это знакомое всем со школы уравнение прямой:
![]() .
.
Здесь α – постоянная составляющая, то есть даже если х = 0 , то Y все равно будет иметь какое-либо положительное или отрицательное значение; β обычно называют коэффициентом регрессии, он отражает наклон линии графика, вдоль которой рассеяны значения Y , выявленные в результате наблюдения за поведением Y , а не в результате расчетов в соответствии с моделью; ε – ошибка или значение помехи, также называемая остатком. Существование остатка может объяснимо либо тем, что кроме рассматриваемого фактора х на значение зависимой переменной могут влиять и другие факторы, неучтенные в модели, либо трудностями измерения х . Математическое ожидание (среднее значение) ошибки ε равно нулю.
В качестве факторной переменной может учитываться показатель времени t . Тогда мы имеем дело с уравнением тренда. В случае с линейным трендом значения t = 1, 2, 3 … n .
Метод наименьших квадратов (МНК, англ. Ordinary Least Squares , OLS ) является одним из основных методов определения параметров регрессионных уравнений, Он заключается в том, чтобы определить вид кривой, характер которой в наибольшей степени соответствует выраженной эмпирическими данными зависимости. Такая кривая должна обеспечить наименьшее значение суммы квадратов отклонений эмпирических значений величин показателя от значений, вычисленных согласно уравнению этой кривой. Меняя вид теоретических кривых, приближенно отображающих динамику рассматриваемого показателя, пытаются добиться как можно меньшего значения этой разности.
Пусть теоретическая зависимость линейна (парная регрессия, прямая в двухмерном пространстве) и выражена регрессионным уравнением:
Коэффициент b можно определить по формуле

Найдем a , подставив в уравнение прямой, параметры которого находим, значение уже известного параметра b и средние значения x ср и Y ср :
![]()
Допустим, связь между двумя показателями парной регрессии выражена функцией
то есть в виде многочлена степени k .
– матрица коэффициентов системы (2.19). В случае, когда величины х
i
(то есть, в различных наблюдениях i
) различны, столбцы матрицы Х
линейно независимы. Тогда вектор-столбец ![]() коэффициентов многочлена Y
(х)
является единственным решением матричного уравнения:
коэффициентов многочлена Y
(х)
является единственным решением матричного уравнения:
![]() ,
,
где ![]() – вектор столбец последовательных значений величины Y
. Отсюда a
(вектор оценок параметров) может быть найден по формуле:
– вектор столбец последовательных значений величины Y
. Отсюда a
(вектор оценок параметров) может быть найден по формуле:
![]() ,
,

Линейная многомерная регрессионная модель (модель множественной линейной регрессии ) является обобщением модели парной линейной регрессии. Она имеет вид:
где Х mt – значение фактора-регрессора Х m в момент наблюдения t , при α 0 вектор независимых переменных Х0 = (1, 1, …, 1) . В этом случае α 0 – так называемый свободный член. Такая модель с учетом допущений, перечисленных выше, называется нормальной линейной регрессионной моделью .
Удобно будет представить формулу (2.23) в матричном виде. Обозначим через Y вектор-столбец значений зависимой переменной (Y 1 , Y2, …, Yn ) ; α вектор-столбец коэффициентов (α 0 , α 1 , α 2 , …, αm ) ; ε – вектор-столбец стохастических компонент (ошибок) (ε 0 , ε 1 , ε 2 , …, εn ) ; Х – матрица независимых переменных размерности nxm :

Получим матричную запись системы, состоящей из уравнений вида
![]() .
.
Отсюда, учитывая обратимость матрицы XTX , находим вектор оценок коэффициентов системы, при чем это будет сделано в соответствии с формулой, в точности повторяющей уже знакомую нам формулу:
![]() .
.
Для обоснованного применения метода наименьших квадратов данные должны соответствовать ряду допущений:
1) Математическая форма зависимости эндогенных переменных от экзогенных переменных модели носит линейный характер (другие типы уравнений, отражающих зависимость значения одной переменной от других, должны быть приведены к линейному виду, прежде чем возможно будет использовать метод наименьших квадратов), и независимые переменные модели являются единственными значимыми факторами, определяющими поведение зависимой переменной;
2) Значение ошибки ε нормально распределено со средней, равной 0 , и постоянной дисперсией , . То есть, хотя значение переменной Y значимо определяется только учтенными в модели факторными признаками, существует также ряд второстепенных факторов, некоторые из которых будут положительно влиять на величину Y , некоторые – отрицательно. В случае множества как положительных, так и отрицательных влияний значение ошибки ε будет нормально распределено. Нормальное распределение полностью определяется двумя параметрами: средней и средним квадратическим отклонением (дисперсией σ 2 ). Чем больше случайных величин действует вместе, тем точнее проявляется закон нормального распределения. Допущение о постоянной дисперсии говорит о постоянности разброса значений ε , вне зависимости от величины значения факторов. Тогда значение ошибки обладает свойством гомоскедастичности . Если разброс значений ошибки ε непостоянен, то имеет место явление гетероскедастичности .
3) Последующие значения ошибок независимы друг от друга, то есть ковариация в парах значений ε равна нулю (cov ε i ε j = 0 ). Это означает, что второстепенные факторы или факторы-причины ошибки для одной из величин Y, не приводят автоматически к ошибкам для всех наблюдений Y . Когда значения ε независимы, то данные неавтокоррелированы. Если же значения ε не являются независимыми, то данные демонстрируют наличие автокорреляции .
4) Независимые переменные являются нестохастическими, то есть их значения для модели детерминированы, заданы изначально.
Процесс построения и использования эконометрических моделей является достаточно сложным и подразумевает следующее:
1) после определения цели исследования необходимо построить систему показателей и логически рассортировать факторы, в наибольшей степени влияющие на каждый показатель;
2) осуществляется выбор формы связи изучаемых показателей между собой и отобранными факторами, другими словами, выбор типа эконометрической модели (линейная, нелинейная, степенная и т. д.);
3) решается проблемы сбора исходных данных и анализа информации;
4) строится эконометрическая модель, то есть определяются ее параметры;
5) проверяется качество построенной модели, в первую очередь ее адекватность изучаемому явлению, после чего модель может быть использована для экономического анализа и прогнозирования.
3.2.3. Отбор переменных эконометрической модели
Особое внимание следует обратить на построение системы показателей и определение совокупности факторов, влияющих на каждый из показателей. К включаемым в эконометрическую модель факторам предъявляются требования:
· включение каждого фактора в модель следует обосновать теоретически;
· целесообразно учитывать только те факторы, которые оказывают существенное влияние на изучаемые показатели, при этом рекомендуется, чтобы количество включаемых в модель факторов не превышало одной трети от числа наблюдений в выборке (длины временного ряда);
· между факторами не должно существовать линейной зависимости, поскольку ее наличие будет означать, что они характеризуют влияние одной и той же по сути причины на показатель. Например, размер заработной платы работников зависит в том числе и от роста производительности труда и от объема выпускаемой продукции. Однако эти два фактора могут быть тесно взаимосвязаны, коррелированны, следовательно в модель целесообразно включить лишь один из них. Включение в модель линейно зависимых факторов приводит к возникновению мультиколлинеарности , которая отрицательно сказывается на качестве модели;
· в одну модель не следует включать какой-либо фактор одновременно с образующими его частными факторами. Это приведет к не соответствующему реальности увеличению их влияния на зависимые переменные модели и, как следствие, к искажению отображения реальной действительности.
При отборе факторов, влияющих на зависимые переменные модели, используются статистические методы отбора. Так, существенного сокращения числа факторов (а значит – сделать модель менее громоздкой) можно достичь с помощью применения пошаговых процедур отбора переменных . Их можно сочетать и с другими подходами к решению проблемы, например, с экспертными методами оценки значимость факторов. Среди пошаговых процедур отбора факторов часто используются процедуры пошагового включения и исключения факторов.
Метод исключения предполагает построение уравнения, включающего некоторую начальную совокупность переменных с последующим последовательным сокращением их числа до тех пор, пока не будет выполнено заданное изначально при составлении уравнения условие. Применение метода включения подразумевает последовательное включение в модель все новых переменных, пока модель не станет соответствовать установленному критерию качества модели. Последовательность включения переменных в модель определяется с помощью частных коэффициентов корреляции: те переменные, для которых значение такого коэффициента, показывающего их связь с исследуемым показателем, больше, чем для прочих, включаются в регрессионное уравнение в первую очередь.
Одним из критериев одновременного включения или невключения нескольких признаков-факторов в модель является их линейная независимость. Если данная предпосылка не выполняется, то возникает явление мультиколлинеарности, то есть наличие сильной корреляции между некоторыми независимыми переменными модели (факторами). В содержательном аспекте мультиколлинеарность приводит к искажению смысла коэффициентов регрессии и затрудненности выявления наиболее влиятельных факторов.
Основные причины мультиколлинеарности: независимые переменные либо характеризуют одно и то же свойство изучаемого явления, либо их влияния являются составными элементами влияния одного и того же признака.
Наиболее распространенным методом выявления мультиколлинеарности является метод корреляции . Устраняют мультиколлинеарность чаще всего исключением одного из таких факторов.
3.2.4. Оценка качества параметров и анализ эконометрической модели
Описывавшиеся выше модели линейной регрессии являются вероятностными, а определяемые на основе метода наименьших квадратов параметры уравнений регрессии – только лишь оценками a и b истинных параметров a и b зависимости эндогенной переменной от некоторых экзогенных. Таким образом, нужно проверить, насколько данные оценки верны относительно истинных коэффициентов. Это осуществляется путем проверки:
статистической значимости коэффициентов регрессии;
близости расположения фактических данных к рассчитанной линии регрессии.
Оценки коэффициентов регрессии так же, как и ошибка (стохастическая компонента уравнения регрессии), предположительно нормально распределены. Статистическая значимость коэффициентов измеряется степенью вариации вокруг оценочного значения. Для измерения величины вариации нормально распределенных ошибок, остатков используется среднее квадратическое отклонение этих остатков – стандартные ошибки коэффициентов. Для определения степени значимости коэффициентов используется t-критерий . Для того чтобы иметь возможность их определить, нужно узнать оценки их дисперсий и, таким образом, средних квадратических отклонений.
После можно проверить гипотезу относительно коэффициентов либо определить для них доверительные интервалы.
Оценки параметров уравнения парной линейной регрессии. Надежность полученных оценок коэффициентов α и β , очевидно, зависит от дисперсии стохастической компоненты уравнения регрессии ε. Однако по данным выборки значений переменных модели дисперсия ε не может быть оценена, то при анализе надежности оценок коэффициентов регрессии используется дисперсия отклонений эмпирических значений переменной Y от рассчитанных на основе полученного уравнения: еi = Yi – a – bxi.
В случае парной линейной регрессии дисперсия b – оценки β равна:

Дисперсия α равна

мера разброса значений зависимой переменной вокруг линии регрессии – так называемая «необъясненная дисперсия», «остаточная дисперсия». Sa и Sb – стандартные отклонения случайных величинa и b . Коэффициент b – коэффициент наклона линии регрессии. Чем больше разброс значений зависимой переменной вокруг линии регрессии, тем большей (в среднем) окажется ошибка в определении наклона линии регрессии. Если же все значения Y расположены на линии регрессии (ei = 0 , а, значит, σ² = 0 ), то ошибки в определении значений коэффициентов a и b отсутствуют (отсюда – s 2 , соответствующее σ² , равно нулю).
Формально значимость оцененного коэффициента регрессии b может быть проверена с помощью анализа его отношения к своему стандартному отклонению ![]() . Эта величина в случае соблюдения исходных предпосылок модели характеризуется t-распределением Стьюдента с n
–2
степенями свободы, где n
– число наблюдений:
. Эта величина в случае соблюдения исходных предпосылок модели характеризуется t-распределением Стьюдента с n
–2
степенями свободы, где n
– число наблюдений:

Для t-статистики проверяется гипотеза о равенстве ее нулю. t = 0 будет означать b = 0 .
При оценке коэффициента линейной регрессии можно использовать следующее грубое правило. Если стандартная ошибка коэффициента больше его модуля (│ t │<1 ), то он не может быть признан «хорошим», значимым, поскольку доверительная вероятность при двусторонней альтернативной гипотезе составляет менее приблизительно 0,7 . Если стандартная ошибка меньше модуля коэффициента, но больше его половины (1<│ t │<2 ), то данная оценка коэффициента может рассматриваться как более или менее значимая (доверительная вероятность от 0,7 до 0,95 ). Значение t от 2 до 3 свидетельствует о наличии весьма значимой связи (доверительная вероятность от 0,95 до 0,99 ), │t│>3 означает практически стопроцентное подтверждение ее наличия. Несомненно, в каждом случае определенную роль играет количество наблюдений: чем их больше, тем надежнее при прочих равных условиях выводы о наличии связи и тем меньше граница доверительного интервала для данного числа степеней свободы и уровня значимости. Однако эти различия существенны лишь для малых n , а при n≥10 сформулированные правила приблизительно верны.
Для осуществления проверки значимости оценок коэффициентов регрессии нужно решить, будет ли она односторонней или двусторонней. Выбор определяется теоретическим обоснованием модели связи зависимой и независимой переменных. При этом односторонняя проверка предполагает, что характер связи между X и Y однозначен: либо связь отрицательна, либо положительна, но не то и другое одновременно. При двусторонней проверке исходят из предположения, что связь между X и Y может быть как положительной, так и отрицательной.
С помощью рассчитанных стандартных отклонений и значений t-статистики можно определить доверительный интервал значений α и β с заданной доверительной вероятностью. Предполагаемые значения α и β будут находиться в рамках этого интервала, если же нет, то придется отвергнуть предположение, выдвинутое относительно величины α и β :
Самым простым типом линии тренда является прямая линия, описываемая линейным (т.е. первой степени) уравнением тренда: где - выровненные, т.е. лишенные колебаний, уровни тренда для лет с номером i;
а - свободный член уравнения, численно равный среднему выровненному уровню для момента или периода времени, принятого за начало отсчета, т.е. для t =0;
b - средняя величина изменения уровней ряда за единицу изменения времени;
ti - номера моментов или периодов времени, к которым относятся уровни временного ряда (год, квартал, месяц, дата).
Среднее изменение уровней ряда за единицу времени - главный параметр и константа прямолинейного тренда. Следовательно, этот тип тренда подходит для отображения тенденции примерно равномерных изменений уровней: равных в среднем абсолютных приростов или абсолютных сокращений уровней за равные промежутки времени.
Графическое изображение прямолинейного тренда - прямая линия в системе прямоугольных координат с линейным (арифметическим) масштабом на обеих осях.
Основные свойства тренд а в форме прямой линии таковы:
Равные изменения за равные промежутки времени;
Если средний абсолютный прирост - положительная величина, то относительные приросты или темпы прироста постепенно уменьшаются;
Если среднее абсолютное изменение - отрицательная величина, то относительные изменения или темпы сокращения постепенно увеличиваются по абсолютной величине снижения к предыдущему уровню;
Если тенденция к сокращению уровней, а изучаемая величина является по определению положительной, то среднее изменение b не может быть больше среднего уровня а;
При линейном тренде ускорение, т.е. разность абсолютных изменений за последовательные периоды, равно нулю.
Параболический тренд и его свойства. Под названием параболического будем иметь в виду тренд, выраженный параболой II порядка с уравнением
=a+b*t+c*t 2
Значения (смысл, сущность) параметров параболы II порядка таковы: свободный член а - это средний (выровненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е. t = 0; b - это средний за весь период среднегодовой прирост, который уже не является константой, а изменяется равномерно со средним ускорением, равным 2 с, которое и служит константой, главным параметром параболы II порядка.
Следовательно, тренд в форме параболы II порядка применяется для отображения таких тенденций динамики, которым свойственно примерно постоянное ускорение абсолютных изменений уровней.
Основные свойства тренда в форме параболы II порядка таковы:
1) неравные, но равномерно возрастающие или равномерно убывающие абсолютные изменения за равные промежутки времени;
2) парабола, рассматриваемая относительно ее математической формы, имеет две ветви: восходящую с увеличением уровней признака и нисходящую с их уменьшением. Но относительно статистики по содержанию изучаемого процесса изменений трендом, выражающим определенную тенденцию развития, чаще всего можно считать только одну из ветвей: либо восходящую, либо нисходящую. В особых, более конкретных, ситуациях мы не отрицаем возможности объединения обеих ветвей в единый тренд;
3) так как свободный член уравнения а как значение показателя в начальный момент (период) отсчета времени, как правило, величина положительная, то характер тренда определяется знаками параметров b и с:
а) при b >0 и с>0 имеем восходящую ветвь, т.е. тенденцию к ускоренному росту уровней;
б) при b <0 и с<0 имеем нисходящую ветвь - тенденцию к ускоренному сокращению уровней;
в) при b > 0 и с<0 имеем либо восходящую ветвь с замедляющимся ростом уровней, либо обе ветви параболы, восходящую и нисходящую, если их по существу можно считать единым процессом;
г) при b <0 и с>0 имеем либо нисходящую ветвь с замедляющимся сокращением уровней, либо обе ветви - нисходящую и восходящую, если их можно считать единой тенденцией;
4) при параболической форме тренда, в зависимости от соотношений между его параметрами, цепные темпы изменений могут либо уменьшаться, либо некоторое время возрастать, но при достаточно длительном периоде рано или поздно темпы роста обязательно начинают уменьшаться, а темпы сокращения уровней при b <0 и с<0 обязательно начинают возрастать (по абсолютной величине относительного изменения).
Экспоненциальным трендом называют тренд, выраженный уравнением: y i =a*k t i . Свободный член экспоненты а равен выровненному уровню, т.е. уровню тренда в момент или период, принятый за начало отсчета времени, т.е. при t= 0. Основной параметр экспоненциального тренда k является постоянным темпом изменения уровней (ценным). Если k> 1, имеем тренд с возрастающими уровнями, причем это возрастание не просто ускоренное, а с возрастающим ускорением и возрастающими производными всех более высоких порядков. Если k< 1, то имеем тренд, выражающий тенденцию постоянного, но замедляющегося сокращения уровней, причем замедление непрерывно усиливается. Экстремума экспонента не имеет и при стремится либо к при k > 1, либо к 0 при k< 1.
Экспоненциальный тренд характерен для процессов, развивающихся в среде, не создающей никаких ограничений для роста уровня. Из этого следует, что на практике он может развиваться только на ограниченном промежутке времени, так как любая среда рано или поздно создает ограничения, любые ресурсы со временем исчерпаемы.
Основные свойства экспоненциального тренда:
1. Абсолютные изменения уровней тренда пропорциональны самим уровням.
2. Экспонента экстремумов не имеет: при k > 1 тренд стремится к + , при k< 1 тренд стремится к 0.
3. Уровни тренда представляют собой геометр прогрессию: уровень периода с номером t =т есть a*k m .
4. При k > 1 тренд отражает ускоряющийся неравномерно рост уровней, при k < 1 тренд отражает замедляющееся неравномерно уменьшение уровней. Поведение основных показателей динамики в этих случаях рассмотрено в табл. 5 и 6.
из различных форм гипербол рассмотрим только наиболее простую:
Если основной параметр гиперболы b>0, то этот тренд выражает тенденцию замедляющегося снижения уровней и при .. Таким образом, свободный член гиперболы - это предел, к которому стремится уровень тренда.
Такая тенденция наблюдается, например (рис. 4), при изучении процесса снижения затрат любого ресурса (труда, материалов, энергии) на единицу данного вида продукции или ее себестоимости в целом. Затраты ресурса не могут стремиться к нулю, значит, экспонента не соответствует сущности процесса; нужно применить гиперболическую формулу тренда.
Если параметр b<0, то с возрастанием t, т.е. с течением времени, уровни тренда возрастают и стремятся к величине а при .Такой характер динамики присущ, например, показателям КПД двигателей или иных преобразователей энергии.
Основные свойства гиперболического тренда:
1. Абсолютный прирост или сокращение уровней, ускорение абсолютных изменений, темп изменения - все эти показатели не являются постоянными. При b>0 уровни замедленно уменьшаются, отрицательные абсолютные изменения, а также положительные ускорения тоже уменьшаются, цепные темпы изменения растут и стремятся к 100%.
2. При b<0 уровни замедленно возрастают, положительные абсолютные изменения, а также отрицательные ускорения и цепные темпы роста замедленно уменьшаются, стремясь к 100%.
Как видим, гиперболический тренд описывает в любом случае тенденцию такого процесса, показатели которого со временем затухают, т.е. происходит переход от движения к застою.
- Граница между европой и азией Америка относится к европе
- Как экономить деньги при маленькой зарплате?
- Порядок получения жилищной субсидии для военнослужащих
- Лимит кассы: нормативная база и сроки установления лимита
- Полная система вычетов Алгебраическая форма комплексного числа
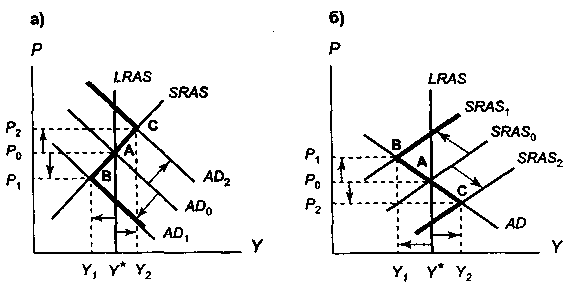
- Модель «Совокупный спрос – совокупное предложение Увеличение совокупного спроса вызывает
- Что называется периодом в физике
- Виды и типы недвижимости, их экономическая составляющая Поля инициализаторов типа
- Экономика, население и города Чеченской Республики
- Особенности проведения региональной программы материнский капитал в московской области Региональный материнский капитал программе семья
- Должностная инструкция страхового агента росгосстрах
- Учет материалов на складе и в бухгалтерии
- На вопрос «Можно ли строить дом без разрешения на строительство?
- Ип на осно какие налоги платит?
- Доходы и расходы будущих периодов Как распределить расходы, затрагивающие несколько налоговых периодов
- Экономические циклы, их особенности и виды
- Необходимо знать от чего зависят цены на жилье
- Контрольная работа: Экономическая мысль Древней Греции
- Бухгалтерские проводки по реализации товаров и услуг 1с бухгалтерия 8
- Оборотные активы организации