Найти сумму числового ряда онлайн с подробным решением. Найти сумму ряда
Поскольку точное значение суммы ряда удается вычислить далеко не всегда (такие задачи были нами рассмотрены), возникает проблема приближенного вычисления суммы ряда с заданной точностью.
Напомним, что
-ый
остаток ряда получается из исходного ряда
получается из исходного ряда отбрасыванием первых
отбрасыванием первых слагаемых:
слагаемых:
Тогда, поскольку для сходящегося ряда
 ,
,
остаток сходящегося ряда равен разности
между суммой ряда и
 -ой
частичной суммой:
-ой
частичной суммой:
 ,
,
и для достаточно больших
 имеем
приближенное равенство
имеем
приближенное равенство
 .
.
Из определения остатка ряда следует,
что абсолютная погрешность при замене
точного неизвестного значения суммы
 его частичной суммой
его частичной суммой равна модулю остатка ряда:
равна модулю остатка ряда:
 .
.
Таким образом, если требуется вычислить
сумму ряда с заданной точностью
 ,
то нужно оставить сумму такого числа
,
то нужно оставить сумму такого числа слагаемых, чтобы для отброшенного
остатка ряда выполнялось неравенство:
слагаемых, чтобы для отброшенного
остатка ряда выполнялось неравенство:
 .
.
Метод приближенного вычисления суммы выбирается в зависимости от вида ряда:
если ряд положительный и может быть исследован на сходимость по интегральному признаку (удовлетворяет условиям соответствующей теоремы), то для оценки суммы используем формулу
 ;
;
если это ряд Лейбница, то применяем оценку:
 .
.
В других задачах можно использовать формулу суммы бесконечно убывающей геометрической прогрессии.
Задача №1.
Сколько нужно взять
слагаемых ряда ,
чтобы получить его сумму с точностью
0,01.
,
чтобы получить его сумму с точностью
0,01.
Решение.
Прежде всего отметим, что
данный ряд сходится. Рассмотрим -ый
остаток ряда, который и является
погрешностью вычислений суммы ряда:
-ый
остаток ряда, который и является
погрешностью вычислений суммы ряда:
Оценим этот ряд с помощью бесконечно
убывающей геометрической прогрессии.
Для этого заменим в каждом слагаемом
множитель
 на
на ,
при этом каждое слагаемое увеличится:
,
при этом каждое слагаемое увеличится:

После вынесения общего множителя за скобку, в скобке остался ряд, составленный из членов бесконечно убывающей геометрической прогрессии, сумму которого мы и вычислили по формуле
 .
.
Заданная точность будет достигнута,
если
 будет удовлетворять условию
будет удовлетворять условию
 .
.
Решим неравенство, учитывая, что
 -
целое.
-
целое.
При
 имеем
имеем
 .
.
При
 имеем
имеем
 .
.
В силу монотонности функции
 ,
неравенство
,
неравенство будет выполняться для всех
будет выполняться для всех .
.
Следовательно, если вместо точного значения суммы мы возьмем первые пять (или более) слагаемых, то погрешность вычислений не превысит 0,01.
Ответ:
 .
.
Задача №2.
Оценить ошибку, получаемую
при замене суммы ряда суммой
первых 100 слагаемых.
суммой
первых 100 слагаемых.
Решение.
Заметим, что данный ряд
является сходящимся и знакопеременным.
Оценивать будем ряд ,
состоящий из модулей исходного ряда,
что сразу увеличивает погрешность
вычислений. Кроме того, нам придется
перейти (используя признак сравнения)
к большему, более простому сходящемуся
ряду:
,
состоящий из модулей исходного ряда,
что сразу увеличивает погрешность
вычислений. Кроме того, нам придется
перейти (используя признак сравнения)
к большему, более простому сходящемуся
ряду:
 .
.
Рассмотрим ряд
 .
Поскольку этот ряд удовлетворяет
условиям теоремы – интегрального
признака сходимости, то для оценки
погрешности вычисления суммы используем
соответствующую формулу:
.
Поскольку этот ряд удовлетворяет
условиям теоремы – интегрального
признака сходимости, то для оценки
погрешности вычисления суммы используем
соответствующую формулу:
 .
.
Вычислим несобственный интеграл:
погрешность вычислений можно оценить по формуле
 ,
,
по условию
 ,
тогда.
,
тогда.
Ответ:
 .
.
Задача №3.
Оценить ошибку,
получаемую при замене суммы ряда суммой
первых 10 слагаемых.
суммой
первых 10 слагаемых.
Решение. Подчеркнем еще раз, что задача о приближенном вычислении суммы имеет смысл только для сходящегося ряда, поэтому, прежде всего отметим, что данный ряд сходится. Поскольку исследуемый ряд является знакопеременным со сложным правилом изменения знака, то оценивать придется, как и в предыдущем примере, ряд из модулей данного ряда:
 .
.
Используя тот факт, что
 при любом значении аргумента, имеем:
при любом значении аргумента, имеем:
 .
.
Оценим остаток ряда:
 .
.
Мы получили ряд, составленный из членов бесконечно убывающей геометрической прогрессии, в которой
 ,
,
его сумма равна:
 ,
,
 .
.
Ответ:
 .
.
Задача №4.
Вычислить сумму ряда с
точностью 0,01.
с
точностью 0,01.
Решение. Данный ряд является рядом Лейбница. Для оценки погрешности верна формула:
 ,
,
другими словами, погрешность вычислений
меньше модуля первого отброшенного
слагаемого. Подберем номер
 так, чтобы
так, чтобы
 .
.
При
 имеем
имеем
 .
.
При
 имеем
имеем
 .
.
Погрешность
 ,
если в качестве значения суммы возьмем
сумму первых четырех слагаемых:
,
если в качестве значения суммы возьмем
сумму первых четырех слагаемых:
Ответ: .
.
Сумма всех натуральных чисел может быть записана с использованием следующего числового ряда

Этот, на первый взгляд, совершенно противоречащий интуиции результат, тем не менее может быть строго доказан. Но прежде, чем говорить о доказательстве, нужно сделать отступление и вспомнить основные понятия.
Начнём с того, что «классической» суммой ряда называется предел частичных сумм ряда, если он существует и конечен. Подробности можно найти в википедии и соответствующей литературе. Если конечный предел не существует, то ряд называется расходящимся.
Например, частичная сумма первых k членов числового ряда 1 + 2 + 3 + 4 +… записывается следующим образом

Нетрудно понять, что эта сумма неограниченно растёт при стремлении k к бесконечности. Следовательно, исходный ряд является расходящимся и, строго говоря, не имеет суммы. Существует, однако, множество способов присвоить конечное значение расходящимся рядам.
Ряд 1+2+3+4+… далеко не единственный из расходящихся рядов. Возьмём, например, ряд Гранди

Который тоже расходится, но известно, что метод суммирования Чезаро позволяет присвоить этому ряду конечное значение 1/2. Суммирование по Чезаро заключается в оперировании не частичными суммами ряда, а их арифметическими средними. Позволив себе порассуждать в вольном стиле, можно сказать, что то частичные суммы ряда Гранди осцилируют между 0 и 1, в зависимости от того какой член ряда является последним в сумме (+1 или -1), отсюда и значение 1/2, как арифметическое среднее двух возможных значений частичных сумм.
Другим интересным примером расходящегося ряда является знакопеременный ряд 1 - 2 + 3 - 4 +... , частичные суммы которого также осцилируют. Суммирование методом Абеля позволяет присвоить данному ряду конечное значение 1/4. Отметим, что метод Абеля является, своего рода, развитием метода суммирования по Чезаро, поэтому результат 1/4 несложно осмыслить с точки зрения интуиции.
Здесь важно отметить, что методы суммирования не являются трюками, которые придумали математики, чтобы как-то совладать с расходящимися рядами. Если вы примените суммирование по Чезаро или метод Абеля к сходящемуся ряду, то ответ, который дают эти методы, равен классической сумме сходящегося ряда.
Ни суммирование по Чезаро, ни метод Абеля, однако, не позволяют работать с рядом 1 + 2 + 3 + 4 +..., т. к. средние арифметические частичных сумм, равно как и средние арифметические средних арифметических, расходятся. Кроме того, если значения 1/2 или 1/4 ещё как-то можно принять и соотнести с соответствующими рядами, то -1/12 сложно связать с рядом 1 + 2 + 3 + 4 +..., представляющим собой бесконечную последовательность положительных целых чисел.
Существует несколько способов прийти к результату -1/12. В этой заметке я лишь кратко остановлюсь на одном из них, а именно регуляризации дзета-функцией . Введём дзета-функцию

Подставляя s = -1 , получим исходный числовой ряд 1+2+3+4+…. Проделаем над этой функцией ряд несложных математических действий
Где является эта-функцией Дирихле
При значении s = -1 эта-функция становится уже знакомым нам рядом 1 - 2 + 3 - 4 + 5 -… «сумма» которого равна 1/4. Теперь мы можем легко решить уравнение
![]()
![]()
Интересно, что этот результат находит своё применение в физике. Например, в теории струн. Обратимся к стр. 22 книги Joseph Polchinski «String Theory»:

Если для кого-то теория струн не является убедительным примером в силу отсутствия доказательств множества следствий этой теории, то можно также упомянуть, что похожие методы фигурируют в квантовой теории поля при попытке рассчитать эффект Казимира .
Чтобы два раза не ходить, ещё пара интересных примеров с дзета-функцией


Для тех, кто захочет получить больше информации по теме отмечу, что написать данную заметку я решил после перевода соответствующей статьи на википедии , где в разделе «Ссылки» вы сможете найти массу дополнительного материала, в основном на английском языке.
И т.д. – достаточно самых минимальных знаний о числовых рядах . Необходимо понимать, что такое ряд , уметь расписывать его подробно и не округлять глаза после словосочетаний «ряд сходится», «ряд расходится», «сумма ряда». Поэтому, если ваше настроение совсем на нуле, пожалуйста, уделите 5-10 минут статье Ряды для чайников (буквально первые 2-3 страницы), а потом возвращайтесь сюда и смело начинайте решать примеры!
Следует отметить, что в большинстве случаев найти сумму ряда непросто, и этот вопрос обычно решается через функциональные ряды
(доживём-доживём:))
. Так, например, сумма популярного артиста ![]() выводится через ряды Фурье
. В этой связи на практике почти всегда требуется установить сам факт сходимости
, но не найти конкретное число (многие, думаю, уже успели это заметить). Однако среди великого множества числовых рядов есть немногочисленные представители, которые позволяют без особых проблем прикоснуться к святая святых даже полному чайнику. И на вводном уроке я приводил пример бесконечно убывающей геометрической прогрессии
выводится через ряды Фурье
. В этой связи на практике почти всегда требуется установить сам факт сходимости
, но не найти конкретное число (многие, думаю, уже успели это заметить). Однако среди великого множества числовых рядов есть немногочисленные представители, которые позволяют без особых проблем прикоснуться к святая святых даже полному чайнику. И на вводном уроке я приводил пример бесконечно убывающей геометрической прогрессии ![]() , сумма которой легко рассчитывается по известной школьной формуле.
, сумма которой легко рассчитывается по известной школьной формуле.
В данной статье мы продолжим рассматривать похожие примеры, кроме того, узнаем строгое определение суммы и попутно познакомимся с некоторыми свойствами рядов. Разомнёмся… да прямо на прогрессиях и разомнёмся:
Пример 1
Найти сумму ряда
Решение
: представим наш ряд в виде суммы двух рядов:
Почему в данном случае так можно сделать? Выполненные действия основаны на двух простейших утверждениях:
1) Если сходятся ряды ![]() , то будут сходиться и ряды, составленные из сумм или разностей соответствующих членов: . При этом существенно то обстоятельство, что речь идёт о сходящихся
рядах. В нашём примере мы заранее знаем
, что обе геометрические прогрессии сойдутся, а значит, без всяких сомнений раскладываем исходный ряд в два ряда.
, то будут сходиться и ряды, составленные из сумм или разностей соответствующих членов: . При этом существенно то обстоятельство, что речь идёт о сходящихся
рядах. В нашём примере мы заранее знаем
, что обе геометрические прогрессии сойдутся, а значит, без всяких сомнений раскладываем исходный ряд в два ряда.
2) Второе свойство ещё очевиднее. Константу можно вынести за пределы ряда: ![]() , и это не повлияет на его сходимость или расходимость и итоговую сумму. Зачем выносить константу? Да просто чтобы она «не мешалась под ногами». Но иногда бывает выгодно этого и не делать
, и это не повлияет на его сходимость или расходимость и итоговую сумму. Зачем выносить константу? Да просто чтобы она «не мешалась под ногами». Но иногда бывает выгодно этого и не делать
Чистовое оформление примера выглядит примерно так:
Дважды используем формулу для нахождения суммы бесконечно убывающей геометрической прогрессии: , где – первый член прогрессии, – основание прогрессии.

Ответ : сумма ряда
Начало решения можно оформить несколько в другом стиле – расписать ряд напрямую и перегруппировать его члены:
Дальше по накатанной.
Пример 2
Найти сумму ряда
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Каких-либо особых изысков здесь нет, но однажды мне попался необычный ряд , который может застать врасплох неискушенного человека. Это… тоже бесконечно убывающая геометрическая прогрессия! Действительно, , и сумма рассчитывается буквально за пару мгновений: ![]() .
.
А сейчас живительный глоток математического анализа, необходимый для решения дальнейших задач:
Что такое сумма ряда?
Строгое определение сходимости/расходимости и суммы ряда в теории даётся через так называемые частичные суммы
ряда. Частичные – значит неполные. Распишем частичные суммы числового ряда ![]() :
:
И особую роль играет частичная сумма «эн» членов ряда:
Если предел частичных сумм числового ряда равен конечному числу: , то такой ряд называют сходящимся , а само число – суммой ряда . Если же предел бесконечен либо его не существует, то ряд называют расходящимся .
Вернёмся к демонстрационному ряду ![]() и распишем его частичные суммы:
и распишем его частичные суммы:
Предел частичных сумм – есть в точности бесконечно убывающая геометрическая прогрессия, сумма которой равна: . Похожий предел мы рассматривали на уроке о числовых последовательностях . Собственно, и сама формула – это прямое следствие вышеизложенных теоретических выкладок (см. 2-ой том матана).
Таким образом, прорисовывается общий алгоритм решения нашей задачи : необходимо составить энную частичную сумму ряда и найти предел . Посмотрим, как это осуществляется на практике:
Пример 3
Вычислить сумму ряда![]()
Решение
: на первом шаге нужно разложить общий член ряда
в сумму дробей. Используем метод неопределённых коэффициентов
:
В результате:
Сразу же
полезно провести обратное действие, выполнив тем самым проверку:
Получен общий член ряда в исходном виде, следовательно, разложение в сумму дробей проведено успешно.
Теперь составим частичную сумму ряда . Вообще это делается устно, но один раз я максимально подробно распишу, что откуда взялось:
Как записать совершенно понятно, но чему равен предыдущий член ? В общий член ряда ![]() ВМЕСТО
«эн» подставляем :
ВМЕСТО
«эн» подставляем :
Почти все слагаемые частичной суммы благополучно сокращаются:
Прямо такие пометки и делаем карандашом в тетради. Чертовски удобно.
Осталось вычислить элементарный предел и узнать сумму ряда:
Ответ :
Аналогичный ряд для самостоятельного решения:
Пример 4
Вычислить сумму ряда![]()
Примерный образец чистового оформления решения в конце урока.
Очевидно, что нахождение суммы ряда – это само по себе доказательство его сходимости (помимо признаков сравнения , Даламбера, Коши и др.), о чём, в частности, намекает формулировка следующего задания:
Пример 5
Найти сумму ряда или установить его расходимость![]()
По внешнему виду общего члена можно сразу сказать, как ведёт себя этот товарищ. Без комплексов. С помощью предельного признака сравнения легко выяснить (причём даже устно), что данный ряд будет сходиться вместе с рядом . Но перед нами редкий случай, когда без особых хлопот рассчитывается ещё и сумма.
Решение
: разложим знаменатель дроби в произведение. Для этого нужно решить квадратное уравнение
:
Таким образом:
Множители лучше расположить в порядке возрастания: .
Выполним промежуточную проверку:
ОК
Таким образом, общий член ряда:![]()
Таким образом: ![]()
Не ленимся:
Что и требовалось проверить.
Запишем частичную сумму «эн» членов ряда, при этом обращаем внимание на тот факт, что «счётчик» ряда «начинает работать» с номера . Как и в предыдущих примерах, надёжнее растянуть кобру на приличную длину:
Однако если мы запишем в одну-две строчки, то всё равно будет довольно трудно сориентироваться в сокращениях слагаемых (их таки 3 в каждом члене). И здесь нам на помощь придёт… геометрия. Заставим плясать змею под свою дудочку:
Да, прямо так и пишем в тетради один член под другим и прямо так их вычёркиваем. Кстати, собственное изобретение. Как понимаете, не от самого лёгкого задания в этой жизни =)
В результате всех сокращений получаем:
И, наконец, сумма ряда:
Ответ :
Пример 8
Вычислить сумму ряда ![]()
Это пример для самостоятельного решения.
Рассматриваемая задача, конечно, не радует нас разнообразием – на практике встречается либо бесконечно убывающая геометрическая прогрессия, либо ряд с дробно-рациональным общим членом и разложимым многочленом в знаменателе (к слову, далеко не каждый такой многочлен даёт возможность найти сумму ряда). Но, тем не менее, иногда попадаются необычные экземпляры, и по сложившейся доброй традиции я завершаю урок какой-нибудь любопытной задачей.
Для того, чтобы вычислить сумму ряда , нужно просто сложить элементы ряда, заданное количество раз. Например:
В приведённом выше примере это удалось сделать очень просто, поскольку суммировать пришлось конечное число раз. Но что делать, если верхний предел суммирования бесконечность? Например, если нам нужно найти сумму вот такого ряда:
По аналогии с предыдущим примером, мы можем расписать эту сумму вот так:
Но что делать дальше?! На этом этапе необходимо ввести понятие частичной суммы ряда . Итак, частичной суммой ряда (обозначается S n ) называется сумма первых n слагаемых ряда. Т.е. в нашем случае:
![]()
Тогда сумму исходного ряда можно вычислить как предел частичной суммы:
Таким образом, для вычисления суммы ряда , необходимо каким-либо способом найти выражение для частичной суммы ряда (S n ). В нашем конкретном случае ряд представляет собой убывающую геометрическую прогрессию со знаменателем 1/3. Как известно сумма первых n элементов геометрической прогрессии вычисляется по формуле:
здесь b 1 - первый элемент геометрической прогрессии (в нашем случае это 1) и q - это знаменатель прогрессии (в нашем случае 1/3). Следовательно частичная сумма S n для нашего ряда равна:

Тогда сумма нашего ряда (S ) согласно определению, данному выше, равна:
![]()
Рассмотренные выше примеры являются достаточно простыми. Обычно вычислить сумму ряда гораздо сложнее и наибольшая трудность заключается именно в нахождении частичной суммы ряда. Представленный ниже онлайн калькулятор, созданный на основе системы Wolfram Alpha, позволяет вычислять сумму довольно сложных рядов. Более того, если калькулятор не смог найти сумму ряда, вероятно, что данный ряд является расходящимся (в этом случае калькулятор выводит сообщение типа "sum diverges"), т.е. данный калькулятор также косвенно помогает получить представление о сходимости рядов.
Для нахождения суммы Вашего ряда, необходимо указать переменную ряда, нижний и верхний пределы суммирования, а также выражение для n -ого слагаемого ряда (т.е. собственно выражение для самого ряда).
- Граница между европой и азией Америка относится к европе
- Как экономить деньги при маленькой зарплате?
- Порядок получения жилищной субсидии для военнослужащих
- Лимит кассы: нормативная база и сроки установления лимита
- Полная система вычетов Алгебраическая форма комплексного числа
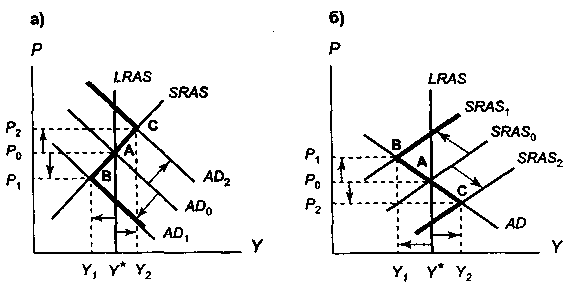
- Модель «Совокупный спрос – совокупное предложение Увеличение совокупного спроса вызывает
- Что называется периодом в физике
- Виды и типы недвижимости, их экономическая составляющая Поля инициализаторов типа
- Экономика, население и города Чеченской Республики
- Особенности проведения региональной программы материнский капитал в московской области Региональный материнский капитал программе семья
- Должностная инструкция страхового агента росгосстрах
- Учет материалов на складе и в бухгалтерии
- На вопрос «Можно ли строить дом без разрешения на строительство?
- Ип на осно какие налоги платит?
- Доходы и расходы будущих периодов Как распределить расходы, затрагивающие несколько налоговых периодов
- Экономические циклы, их особенности и виды
- Необходимо знать от чего зависят цены на жилье
- Контрольная работа: Экономическая мысль Древней Греции
- Бухгалтерские проводки по реализации товаров и услуг 1с бухгалтерия 8
- Оборотные активы организации