Бенуа Мандельброт — его фракталы и их применение в форекс анализе. Бенуа Мандельброт
Существует бесконечное множество различных фракталов. Один из них носит имя Мандельброта. Фрактал Мандельброта – это множество точек на комплексной плоскости, для которых итеративная последовательность
при начальном
условии
 ,
не уходит в бесконечность.
,
не уходит в бесконечность.

Рис. 3.6. Фрактал Мандельброта
Впервые множество
Мандельброта было описано в 1905 году
Пьером Фату
(Pierre Fatou
),
французским математиком, работавшим в
области аналитической динамики
комплексных чисел. Фату изучал рекурсивные
процессы вида (3.2). Начав с точки
 на комплексной плоскости, можно получить
новые точки, последовательно применяя
к ним эту формулу. Такая последовательность
точек называетсяорбитой
на комплексной плоскости, можно получить
новые точки, последовательно применяя
к ним эту формулу. Такая последовательность
точек называетсяорбитой
 при преобразовании (3.2).
при преобразовании (3.2).
Фату нашел, что
орбита
 при этом преобразовании показывает
достаточно сложное и интересное
поведение. Существует бесконечное
множество таких преобразований – своё
для каждого значенияc
.
В те времена компьютеров ещё не было, и
Фату, конечно, не мог построить орбиты
всех точек плоскости, ему приходилось
всё делать вручную. Основываясь на своих
расчётах, он доказал, что орбита
точки, лежащей на расстоянии больше 2
от начала координат, всегда уходит в
бесконечность
.
при этом преобразовании показывает
достаточно сложное и интересное
поведение. Существует бесконечное
множество таких преобразований – своё
для каждого значенияc
.
В те времена компьютеров ещё не было, и
Фату, конечно, не мог построить орбиты
всех точек плоскости, ему приходилось
всё делать вручную. Основываясь на своих
расчётах, он доказал, что орбита
точки, лежащей на расстоянии больше 2
от начала координат, всегда уходит в
бесконечность
.
Фату никогда не видел изображений, которые мы сейчас знаем как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную. Профессор Бенуа Мандельброт был первым, кто использовал для этого компьютер. Фракталы были описаны Мандельбротом в 1975 году в его книге «Les Objets Fractals: Forme, Hasard et Dimension» («Фрактальные объекты: форма, случайность и размерность»). В этой книге Мандельброт впервые использовал термин «фрактал» для обозначения математического феномена, демонстрирующего столь непредсказуемое и удивительное поведение. Эти феномены рождались при использовании рекурсивного алгоритма для получения какой-либо кривой или множества. Множество Мандельброта – один из таких феноменов, названный по имени своего исследователя.
Если использовать
обозначения
 и
и ,
где
,
где – мнимая единица, то итеративная
последовательность (3.2) преобразуется
в:
– мнимая единица, то итеративная
последовательность (3.2) преобразуется
в:
 (3.3)
(3.3)
На рис 3.6.показан графический образ фрактала Мандельброта (на комплексной плоскости). Как обычно, действительная ось расположена горизонтально, а мнимая – вертикально. Закрашенная черным область – это и есть множество Мандельброта. Оттенки белого и голубого соответствуют его дополнению к множеству комплексных чисел. Белым цветом обозначены точки с координатами p и q , которые достаточно «медленно» уходят в бесконечность, синим цветом – точки, которые «быстро» уходят в бесконечность.
Визуально, внутри множества Мандельброта можно выделить бесконечное количество элементарных фигур, причём, самая большая в центре представляет собой кардиоиду . Также есть набор овалов, касающихся кардиоиды, размер которых постепенно уменьшается, стремясь к нулю. Каждый из этих овалов имеет свой набор меньших овалов, диаметр которых также стремится к нулю и т. д. Этот процесс продолжается бесконечно, образуя фрактал. Также важно, что эти процессы ветвления фигур не исчерпывают полностью множество Мандельброта: если рассмотреть с увеличением дополнительные «ветки», то в них можно увидеть свои кардиоиды и круги, не связанные с главной фигурой.
Чтобы построить
изображение фрактала Мандельброта,
подобное тому, что показано на рис. 3.6,
необходимо использовать алгоритм (3.3)
и теорему Фату. Сравнение
 с числом 2 (в англоязычной литературе
его называют «bail-out
»)
позволяет выделять точки, не попадающие
внутрь множества. Для точек, лежащих
внутри множества, последовательность
не будет иметь тенденции к бесконечности
и никогда не достигнет этого числа,
поэтому после определённого числа
итераций расчёт необходимо принудительно
завершить. Максимальное число итераций,
после которых число считается попавшим
внутрь множества, задается в программе.
с числом 2 (в англоязычной литературе
его называют «bail-out
»)
позволяет выделять точки, не попадающие
внутрь множества. Для точек, лежащих
внутри множества, последовательность
не будет иметь тенденции к бесконечности
и никогда не достигнет этого числа,
поэтому после определённого числа
итераций расчёт необходимо принудительно
завершить. Максимальное число итераций,
после которых число считается попавшим
внутрь множества, задается в программе.
Изображение, полученное таким способом, является лишь приближением к реальному множеству Мандельброта. Более качественные результаты можно получать, увеличивая максимальное количество итераций, однако при этом пропорционально возрастает и время расчётов.
Строго математически, изображение множества Мандельброта должно быть чёрно-белым. Точка либо попадает внутрь множества, либо нет. Несмотря на это, с помощью компьютера мы можем построить и цветные изображения. Самым распространённым способом является раскрашивание точек снаружи множества в цвет, равный количеству итераций, за которое точка уходит в «бесконечность» или, с точки зрения программы, на определённое расстояние от нуля.
Существует бесконечное множество различных фракталов. Один из них носит имя Мандельброта. Фрактал Мандельброта – это множество точек на комплексной плоскости, для которых итеративная последовательность
при начальном условии , не уходит в бесконечность.

Рис. 3.6. Фрактал Мандельброта
Впервые множество Мандельброта было описано в 1905 году Пьером Фату (Pierre Fatou ), французским математиком, работавшим в области аналитической динамики комплексных чисел. Фату изучал рекурсивные процессы вида (3.2). Начав с точки на комплексной плоскости, можно получить новые точки, последовательно применяя к ним эту формулу. Такая последовательность точек называется орбитой при преобразовании (3.2).
Фату нашел, что орбита при этом преобразовании показывает достаточно сложное и интересное поведение. Существует бесконечное множество таких преобразований – своё для каждого значения c . В те времена компьютеров ещё не было, и Фату, конечно, не мог построить орбиты всех точек плоскости, ему приходилось всё делать вручную. Основываясь на своих расчётах, он доказал, что орбита точки, лежащей на расстоянии больше 2 от начала координат, всегда уходит в бесконечность .
Фату никогда не видел изображений, которые мы сейчас знаем как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную. Профессор Бенуа Мандельброт был первым, кто использовал для этого компьютер. Фракталы были описаны Мандельбротом в 1975 году в его книге «Les Objets Fractals: Forme, Hasard et Dimension» («Фрактальные объекты: форма, случайность и размерность»). В этой книге Мандельброт впервые использовал термин «фрактал» для обозначения математического феномена, демонстрирующего столь непредсказуемое и удивительное поведение. Эти феномены рождались при использовании рекурсивного алгоритма для получения какой-либо кривой или множества. Множество Мандельброта – один из таких феноменов, названный по имени своего исследователя.
Если использовать обозначения и , где – мнимая единица, то итеративная последовательность (3.2) преобразуется в:
 (3.3)
(3.3)
На рис 3.6.показан графический образ фрактала Мандельброта (на комплексной плоскости). Как обычно, действительная ось расположена горизонтально, а мнимая – вертикально. Закрашенная черным область – это и есть множество Мандельброта. Оттенки белого и голубого соответствуют его дополнению к множеству комплексных чисел. Белым цветом обозначены точки с координатами p и q , которые достаточно «медленно» уходят в бесконечность, синим цветом – точки, которые «быстро» уходят в бесконечность.
Визуально, внутри множества Мандельброта можно выделить бесконечное количество элементарных фигур, причём, самая большая в центре представляет собой кардиоиду . Также есть набор овалов, касающихся кардиоиды, размер которых постепенно уменьшается, стремясь к нулю. Каждый из этих овалов имеет свой набор меньших овалов, диаметр которых также стремится к нулю и т. д. Этот процесс продолжается бесконечно, образуя фрактал. Также важно, что эти процессы ветвления фигур не исчерпывают полностью множество Мандельброта: если рассмотреть с увеличением дополнительные «ветки», то в них можно увидеть свои кардиоиды и круги, не связанные с главной фигурой.
Чтобы построить изображение фрактала Мандельброта, подобное тому, что показано на рис. 3.6, необходимо использовать алгоритм (3.3) и теорему Фату. Сравнение ![]() с числом 2 (в англоязычной литературе его называют «bail-out
») позволяет выделять точки, не попадающие внутрь множества. Для точек, лежащих внутри множества, последовательность не будет иметь тенденции к бесконечности и никогда не достигнет этого числа, поэтому после определённого числа итераций расчёт необходимо принудительно завершить. Максимальное число итераций, после которых число считается попавшим внутрь множества, задается в программе.
с числом 2 (в англоязычной литературе его называют «bail-out
») позволяет выделять точки, не попадающие внутрь множества. Для точек, лежащих внутри множества, последовательность не будет иметь тенденции к бесконечности и никогда не достигнет этого числа, поэтому после определённого числа итераций расчёт необходимо принудительно завершить. Максимальное число итераций, после которых число считается попавшим внутрь множества, задается в программе.
Изображение, полученное таким способом, является лишь приближением к реальному множеству Мандельброта. Более качественные результаты можно получать, увеличивая максимальное количество итераций, однако при этом пропорционально возрастает и время расчётов.
Строго математически, изображение множества Мандельброта должно быть чёрно-белым. Точка либо попадает внутрь множества, либо нет. Несмотря на это, с помощью компьютера мы можем построить и цветные изображения. Самым распространённым способом является раскрашивание точек снаружи множества в цвет, равный количеству итераций, за которое точка уходит в «бесконечность» или, с точки зрения программы, на определённое расстояние от нуля.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Все темы данного раздела:
Счетные и несчетные числовые множества
Теория множеств появилась в конце 19 века благодаря работам немецкого математика Георга Кантора (1845-1918). Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики.
Позиционные и непозиционные системы
Системой счисления называется метод записи чисел в виде комбинаций графических символов. Число – это некоторая абстрактная сущность для описания количества, а цифры – знаки, ис
Десятичная система
Существуют различные позиционные системы исчисления, отличающиеся между собой количеством используемых знаков. Чтобы различать числа в разных системах исчисления, в конце числа ставят индекс – симв
Двоичная система
Двоичная (бинарная) система счисления является самой простой из всех позиционных систем. Она содержит только два символа 0 и 1, и используется в компьютерной технике благодаря своей простоте и высо
Код Грея
Помимо двоичных чисел на практике применяются и другие коды, использующие два знака: 0 и 1. В этом разделе мы познакомимся с кодом Грея. При сортировке данных естественным представлением является о
Троичная система счисления
Троичная система счисления– позиционная система счисления с целочисленным основанием равным 3. Она существует в двух вариантах: несимметричная и симметричная трои
Восьмеричная и шестнадцатеричная системы счисления
Позиционную систему счисления можно построить по любому основанию. Однако наибольшее практическое значение имеют: двоичная, десятичная, восьмеричная и шестнадцатеричная. Причем, последние две испол
Канторово множество
Математика изобилует парадоксальными объектами. Одним из них является канторово множество. Оно описывается следующим образом. Рассмотрим единичный отрезок, показанный на рис. 3.1. Удалим из
Ковер Серпинского и снежинка Коха
Ковер Серпинского получается из единичного квадрата удалением средней части (1/3, 2/3)*(1/3, 2/3), затем удалением из каждого квадрата (i/3, i+1/3)*(j/3, j+1/3) с
Стохастические фракталы
Стохастические фракталы получаются в том случае, если в итерационном процессе случайным образом менять какие-либо параметры. При этом получаются объекты, очень похожие на природные – несимметричные
Энтропийная размерность
Пусть X – компактное пространство с метрикой d. Тогда множество называется r-плотным
Виды доказательства
Древние греки сформулировали основные правила логического доказательства. Они различали два вида доказательства: дедукцию и индукцию. Дедукция – это доказательство от общего
Переменные и формулы в исчислении высказываний
Переменная, значениями которой являются высказывания, называется пропозициональной переменной. Понятие пропозициональной формулы вводится по индукции
Булевы функции
Функция, у которой аргументы пробегают множество {0,1} и которая принимает значение из того же множества
Предикаты
Применяемые в математике высказывания обычно представляют собой описание свойств каких-либо математических объектов или описаний отношений, существующих между этими объектами. Для анализа закономер
Семантика исчисления предикатов
Исчисление предикатов (так же как и исчисление высказываний) являются, прежде всего, языками. И эти языки можно применять не только в математике. Используя их слова, фразы и предложения, мы можем п
Равно(плюс(два, три), пять)
«Некоторые люди любят грибы»
X(личность(Х)
Правила логического вывода
Возможность логически выводить новые правильные выражения из набора истинных утверждений – это важное свойство исчисления предикатов. Логически выведенные выражения корректны, потому что они совмес
Правило резолюции
Правило резолюции (лат. resolutio – решение): если выражения PA
Парадокс Рассела
Задание множеств характеристическим предикатом может приводить к противоречиям. Например, все рассмотренные в примерах множества не содержат себя в качестве элемента. Рассмотрим множество всех множ
Сравнение множеств
Множество содержится в множестве
Свойства операций над множествами
Пусть задан универсум. Тогда
Проблема континуума
Кантор был первым, кто стал рассматривать мощности (кардинальные числа) бесконечных множеств. Мощность счетного множества он обозначил древнееврейской буквой «алеф» с нулевым индексом:
Сумма нечетных чисел
Математическая индукция играет огромную роль в дискретной математике (именно в силу ее дискретного характера). Полученные этим методом доказательства в данной области математики почти столь же наде
Сумма натуральных чисел
А теперь используем метод индукции для доказательства того, что сумма первых n положительных целых чисел равна
Снова считаем подмножества
Доказывая теорему 5.1. мы неявно пользовались методом математической индукции. Теперь пришло время применить его явно. Итак, мы подозреваем, что число всех подмножеств множества из n элемент
Биномиальные коэффициенты
Слово бином означает выражение, состоящее из двух членов, например: x + y. Бином является частным случаем полинома. Биномом Ньютона наз
Треугольник Паскаля
Французский математик Блез Паскаль (1623-1662) составил таблицу из биномиальных коэффициентов. Она получилась треугольной, поскольку с увеличением степени бинома количество коэффициентов также увел
Бином Ньютона для дробных и отрицательных показателей
Формула бинома Ньютона (6.1) для целых положительных показателей была известна задолго до Исаака Ньютона (1643-1727), но им в 1676 году была указана возможность распростране
Гамма-функция
Биномиальная теорема определяет биномиальные коэффициенты через факториалы чисел n и k:
Размещения без повторений
Общее число размещений без повторений из n элементов по k элементов обычно обозначается так:
Сочетания без повторений
Число различных сочетаний без повторений обычно обозначается так: . Или так
Размещения с повторением
Если мы выбираем из множества n элементов размещения с повторениями k элементов, то в данном случае k может превосходить n.
Теорема 7.3. Об
Сочетания с повторением
Теорема 7.4. Общее число сочетаний с повторениями k элементов, взятых из совокупности n различных элементов, равно
Формула Стирлинга
Рассматривая комбинаторные задачи, мы часто сталкиваемся с факториалами. Факториал – это очень быстро растущая функция, она растет быстрее экспоненты. При достаточно больших n (n >
Подстановки
Взаимно однозначная функция называется подстановкой на
Задача Фибоначчи
Итальянский математик Леонардо Фибоначчи жил в 13 столетии и одним из первых в Европе стал использовать арабские (индийские) цифры. Он придумал несколько искусственную задачу о кроликах, которых вы
Шифрование с открытым ключом производится следующим образом. 1. Получателем сообщений производится генерация открытого ключа (пара чисел n и e) и закрытого ключа (число d
Все мы живем в реальности своих идей. Рынок – это зеркало, отражающее наши собственные представления. Каждый человек, связанный с рынком, никогда не имеет дело с реальностью, а всегда лишь со своими представлениями. Иногда представления обретают массовый характер, и мы говорим о трендах, линиях поддержки или графических фигурах. Аналитики часто замечают, что «рост прибыли привел к покупке акций», а «нефть снизилась на продажах инвесторов».
Но в действительности никто из нас не знает, что происходит. Все мы пользуемся лишь моделью, упрощенной версией, копией рынка. Наш успех зависит исключительно от того, насколько наша копия похожа на оригинал.
Начало 21 века серьезно пошатнуло все современные финансовые теории. Банкротство крупных инвестиционных корпораций, финансовый кризис — все это поставило под сомнение те модели, которыми пользовались аналитики и всего мира. Инвестиционные консультанты либо разводят руками, либо упорно держатся за устаревшие теории, но реальность уже нельзя игнорировать – рынки не описываются теорией случайных блужданий, кривой Гаусса, моделью Марковица и формулой Блэка-Шольца.
Копия оказалась грубой подделкой.
Именно поэтому интерес к альтернативным теориям, описывающим поведение финансового рынка, стал стремительно нарастать.
Одной из таких теорий, о которой мы поговорим сегодня, является фрактальная геометрия
. Теория эта уже не нова и активно применяется в разных областях деятельности.
Фрактальная геометрия
Термин «фракталы» у российских трейдеров традиционно связан с именем Билла Вильямса. «Фракталы Вильямса» знают все и они даже включены в список индикаторов известной платформы MetaTrader 4. Но мало кто знает имя настоящего автора этого понятия — Бенуа Мандельброта, известного математика, создателя фрактальной геометрии. Возможно, этой статьи никогда бы не было, если бы Бенуа Мандельброт не занялся всерьез применением фракталов на финансовых рынках.
Итак, что же такое фрактал?
Фрактал – это форма или «структура», которая обладает свойством к самоповторению в разных масштабах . Самый лучший способ объяснить этот термин – показать на примере. Посмотрите на рисунок 1. Что вы видите?
Ваше внимание, очевидно, отметило общую треугольную форму фигуры. Если присмотреться ближе, мы увидим, что треугольник в свою очередь состоит из еще трех вписанных в него треугольников, в каждый из которых вписано еще по три меньших треугольника, и так далее.
Приведенный пример – популярная фигура, известная также как «салфетка Серпинского»
. На любом уровне фигуры каждый ее элемент подобен элементу на более низком или более высоком масштабе. Строительный материал для фрактала или форма, лежащая в его основе, называется «инициатором»
, структура же или самоповторяющийся рисунок – «генератором»
. Инициатором для «салфетки Серпинского» может быть точка, а генератором – треугольник.
Но что это нам дает для понимания финансовых рынков?
Наблюдение 1. Описание рынка с помощью фракталов
Как оказалось, поведение рынка может быть описано с помощью . Самый базовый графический элемент рынка – это прямая линия, направленная сверху вниз или снизу вверх. Каждому трейдеру это хорошо понятно – цена либо растет, либо падает, этот процесс происходит во времени.
Таким образом, у нас появляется инициатор, который выглядит следующим образом (см. рис. 2, 3).

Даже если мы возьмем движение цены в рамках одной минуты, мы все равно получим линию, которая соединяет цену открытия и цену закрытия. Генератором же для движения цены является другая распространенная структура, хорошо известная трейдеру, – «импульс-коррекция-импульс» , которая выглядит, как представлено ниже (см. рис. 4, 5).

Генераторов на рынке может быть бесконечное множество, и точек перелома может быть вовсе не две. Какую же информацию могут дать трейдеру эти фигуры?
Если посмотреть на движение цены отдельного инструмента, можно увидеть, что структура генератора повторяется на всех временных масштабах инструмента. Примем за данность, что внутригодовое движение цены представляет собой простую структуру из двух импульсов и одной как на рисунке 2 или 3. Если оба импульса и коррекцию заменить соответствующими фракталами (генераторами), мы получим следующую структуру (см. рис. 6):

Переходя все глубже и глубже, мы дойдем до минутных, а затем и тиковых графиков, на которых вновь и вновь будет проявляться базовый фрактал .
Что характерно, соотношения между линиями генератора будут оставаться фиксированными на любой временной структуре. Углы между линиями генератора на минутном и месячном графике будет соответствовать друг другу, соотношение их длинны также. Это удивительное открытие дает нам совершенно новый взгляд на привычное движение цены.
Конечно, это понимание является упрощенным, и, по мнению самого Мандельброта, «карикатурным». Оно служит нам для описания общего принципа структуры ценового движения. Реальный рыночный генератор может быть гораздо сложнее.
В моделировании поведения рынка Мандельброт использует более сложную «мультифрактальную» модель, которая использует три измерения и так называемый «фрактальный куб» . На нем мы не будем подробно останавливаться. Вместо этого рассмотрим два других наблюдения фрактальной геометрии, которые более просты для понимания и дают трейдеру пищу для размышлений.
Наблюдение 2. Рынок имеет память
Обширные исследования рынка хлопка привели Бенуа Мандельброта к следующему выводу: периоды высокой волатильности или «турбулентности» имеют тенденцию собираться в «кластеры».

Что же представляет собой «ценовой кластер» ? Я уверен, вы догадались, что это «тренд». Для нас с вами, как трейдеров, это, безусловно, хорошая новость. Пока существуют тренды, работа трейдера будет неплохо оплачиваться.
Наблюдение 3. Эффект «Ноя»
И, наконец, третье наблюдение Мандельброта состоит в так называемом эффекте «Ноя» . Из ветхого завета мы знаем, что всемирный потоп начался неожиданно, и разрушительная сила его оказалась очень велика. Эффект «Ноя» — метафора, характеризующая рыночные развороты – биржевые панические обвалы и взлеты . Они никогда не происходят плавно, почти всегда рынок взмывает вверх или обваливается с такой силой, которую никто из инвесторов не ожидал.
Это всегда вызывает панику среди биржевой публики, которая шокирована такими движениями цены. Так, в 1987 году индекс Доу-Джонса упал на 22.6% за один день. После краха во всем обвиняли компьютерные программы, но у Бенуа Мандельброта совсем другое мнение – дело вовсе не в программах, дело в самой природе рынка
. Именно внутренне присущий рынку характер обуславливает такую динамику. Эта гипотеза также является новой и не согласуется с гипотезой эффективного рынка, согласно которой рынок должен меняться плавно и последовательно.
Об этом свойстве рынка следует помнить трейдерам, которые работают без «стопов», уповая на то, что рынок рано или поздно вернется к уровню открытия сделки.
Выводы
Резюме, которое делает Мандельброт, состоит в следующем: рынок – очень рискованное место, гораздо более рискованное, чем принято считать. Для трейдеров риск – не источник опасности, а потенциальный источник прибыли. Если правильно использовать знания о движении цен и оказываться на «правильной» стороне риска, он будет благом, а не проклятием.
Мир огромен и многообразен, существует колоссальное количество форм и размеров. Люди давно научились измерять. Математика многократно ускорила прогресс, но все же классическая геометрия со своими стандартными фигурами не позволяет описывать замысловатые формы
природы.
В 70ых годах прошлого века нашелся математик Бенуа Мандельброт , который выявил порядок казалось бы, в хаотичных объектах, Мандельброт назвал их фракталами (лат. fractus - сломанный, разбитый). Суть фрактала в самоподобии, в бесконечном повторении собственной формы. Увеличивая масштаб вы всегда будете видеть фигуры аналогичные исходной. Еще В начале 20го века швед Хельге фон Кох построил кривую, которую теперь называют «Снежинка Коха». Он взял треугольник, разбил стороны на равные части и приложил к ним более мелкие треугольники, затем повторил процесс множество раз. На первый взгляд замкнутая кривая, но теоретически
её длина бесконечна. Зависит от размерности объекта и от количества повторений.
Во времена Коха чертили вручную, а вот Мандельброту повезло больше. Мощности ЭВМ хватило для проведения миллионов операций. Получались интересные изображения, одно из них называется: «множество Мандельброта».
Всё вокруг имеет необыкновенную структуру, жизнь выбрала эту форму как оптимальную. Органы: «легкие, почки, кровеносные сосуды, нейроны, все клетки». Также растения: «деревья, кустарники, травы, цветы и плоды, от мельчайших организмов до самых крупных». Твердые материалы, разнообразные вихревые перемещения веществ, жидкостей, газов. Горы, облака, снежинки, молнии, всевозможные явления природы…
Фракталы применяют в компьютерной графике и дизайне
Сотовые
телефоны производят с антеннами фрактального типа. Фрактальная геометрия открывает много нового в биологии, географии и т.д. В будущем практическое применение этой науки будет только расти.
Мандельброт Фрактальная геометрия природы
Энциклопедичный YouTube
1 / 5
✪ Число Пи и множество Мандельброта
✪ Множество Мандельброта | Vsauce на русском
✪ Урок 34. C++ Рисуем фрактал Мандельброта
✪ Бенуа Мандельброт: Фракталы и искусство изломанности
✪ Times Tables, Mandelbrot and the Heart of Mathematics
Субтитры
Расширенное определение
Таким образом, вышеуказанная последовательность может быть раскрыта для каждой точки c {\displaystyle c} на комплексной плоскости следующим образом:
c = x + i ⋅ y {\displaystyle c=x+i\cdot y} Z 0 = 0 {\displaystyle Z_{0}=0} Z 1 = Z 0 2 + c = x + i y {\displaystyle {\begin{matrix}Z_{1}&=&Z_{0}^{2}+c\\\ &=&x+iy\end{matrix}}} Z 2 = Z 1 2 + c = (x + i y) 2 + x + i y = x 2 + 2 i x y − y 2 + x + i y = x 2 − y 2 + x + (2 x y + y) i {\displaystyle {\begin{matrix}Z_{2}&=&Z_{1}^{2}+c\\\ &=&(x+iy)^{2}+x+iy\\\ &=&x^{2}+2ixy-y^{2}+x+iy\\\ &=&x^{2}-y^{2}+x+(2xy+y)i\end{matrix}}} Z 3 = Z 2 2 + c = . . . {\displaystyle Z_{3}=Z_{2}^{2}+c=...}Если переформулировать эти выражения в виде итеративной последовательности значений координат комплексной плоскости x {\displaystyle x} и y {\displaystyle y} , то есть заменив z n {\displaystyle z_{n}} на x n + i ⋅ y n {\displaystyle x_{n}+i\cdot y_{n}} , а c {\displaystyle c} на p + i ⋅ q {\displaystyle p+i\cdot q} , мы получим:
x n + 1 = x n 2 − y n 2 + p {\displaystyle x_{n+1}={x_{n}}^{2}-{y_{n}}^{2}+p} y n + 1 = 2 x n y n + q {\displaystyle y_{n+1}=2{x_{n}}{y_{n}}+q}Визуально, внутри множества Мандельброта можно выделить бесконечное количество элементарных фигур, причём самая большая в центре представляет собой кардиоиду . Также есть набор овалов, касающихся кардиоиды, размер которых постепенно уменьшается, стремясь к нулю. Каждый из этих овалов имеет свой набор меньших овалов, диаметр которых также стремится к нулю и т. д. Этот процесс продолжается бесконечно, образуя фрактал. Также важно, что эти процессы ветвления фигур не исчерпывают полностью множество Мандельброта: если рассмотреть с увеличением дополнительные «ветки», то в них можно увидеть свои кардиоиды и круги, не связанные с главной фигурой. Самая большая фигура (видимая при рассматривании основного множества) из них находится в области от −1,78 до −1,75 на отрицательной оси действительных значений.
История множества Мандельброта
Впервые множество Мандельброта было описано в 1905 году Пьером Фату (Pierre Fatou), французским математиком, работавшим в области аналитической динамики комплексных чисел . Фату изучал рекурсивные процессы вида
Начав с точки на комплексной плоскости, можно получить новые точки, последовательно применяя к ним эту формулу. Такая последовательность точек называется орбитой z 0 {\displaystyle z_{0}} при преобразовании z → z 2 + c {\displaystyle z\to z^{2}+c}
Фату нашел, что орбита z 0 = 0 {\displaystyle z_{0}=0} при этом преобразовании показывает достаточно сложное и интересное поведение. Существует бесконечное множество таких преобразований - своё для каждого значения c {\displaystyle c} . В те времена компьютеров ещё не было, и Фату, конечно, не мог построить орбиты всех точек плоскости, ему приходилось всё делать вручную. Основываясь на своих расчётах, он доказал, что орбита точки, лежащей на расстоянии больше 2 от начала координат, всегда уходит в бесконечность.
Фату никогда не видел изображений, которые мы сейчас знаем как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную. Профессор Бенуа Мандельброт был первым, кто использовал для этого компьютер .
Фракталы были описаны Мандельбротом в 1975 году в его книге «Les Objets Fractals: Forme, Hasard et Dimension» («Фрактальные объекты: форма, случайность и размерность»). В этой книге Мандельброт впервые использовал термин «фрактал» для обозначения математического феномена, демонстрирующего столь непредсказуемое и удивительное поведение. Эти феномены рождались при использовании рекурсивного алгоритма для получения какой-либо кривой или множества. Множество Мандельброта - один из таких феноменов, названный по имени своего исследователя.
Построение множества
Несложно доказать, что как только модуль z n окажется больше 2 (или, в терминах действительной и мнимой частей, x n 2 +y n 2 >4), последовательность станет стремиться к бесконечности. В случае |c |≤2 это можно доказать с помощью метода математической индукции . При |c |>2 точка c заведомо не принадлежит множеству Мандельброта, что также можно вывести методом индукции, используя равенство z 0 =0. (Хотя в этом случае может существовать другое z 0 , для которого соответствующая последовательность ограничена по модулю, но для некоторого n выполняется неравенство |z n |>2.)
Сравнение |z n | с этим числом (в англоязычной литературе его называют «bail-out») позволяет выделять точки, не попадающие внутрь множества. Для точек, лежащих внутри множества, последовательность не будет иметь тенденции к бесконечности и никогда не достигнет этого числа, поэтому после определённого числа итераций расчёт необходимо принудительно завершить. Максимальное число итераций, после которых число считается попавшим внутрь множества, задается в программе.
Изображение, полученное таким способом, является лишь приближением к реальному множеству Мандельброта. Более качественные результаты можно получать, увеличивая максимальное количество итераций, однако при этом пропорционально вырастает и время расчётов.
Добавление цвета
Строго математически, изображения множеств Мандельброта и Жюлиа должны быть чёрно-белыми. Точка либо попадает внутрь множества, либо нет. Несмотря на это, с помощью компьютера мы можем построить и цветные изображения. Самым распространённым способом является раскрашивание точек снаружи множества в цвет, соответствующий количеству итераций, за которое точка уходит в «бесконечность» или, с точки зрения программы, на определённое расстояние от нуля.
Порядок определения, попадает ли точка z 0 внутрь множества (традиционно закрашиваемого чёрным цветом) или нет (закрашивается цветом, зависящим от скорости движения к бесконечности) следующий: на каждой итерации для z n =x n +y n·i вычисляется значение модуля | z n | = x n 2 + y n 2 {\displaystyle |z_{n}|={\sqrt {x_{n}^{2}+y_{n}^{2}}}} , которое затем сравнивается с «границей бесконечности» (обычно берётся значение, равное 2). Здесь важно обратить внимание, что уже на данном этапе можно ввести определённую оптимизацию вычислений, если проверять не x n 2 + y n 2 > 2 {\displaystyle {\sqrt {x_{n}^{2}+y_{n}^{2}}}>2} , а x n 2 + y n 2 > 4 {\displaystyle x_{n}^{2}+y_{n}^{2}>4} , что значительно снизит время расчётов.
Таким образом, если |z n | 2 ≤ 4 при любом числе итераций (на практике - при всех вычисленных итерациях), то цвет точки чёрный, в противном случае он зависит от последнего значения n , при котором |z n | 2 ≤ 4. Значение n , фактически, обозначает скорость движения z n в бесконечность, и может быть просто индексом в таблице цветов, или использоваться как параметр в более сложном алгоритме.
Данный алгоритм определяет, что если точка удаляется больше чем на 2 от начала координат, то она лежит снаружи множества Мандельброта. Для того, чтобы определить, что точка лежит внутри множества есть много способов. Самое простое решение - ограничить количество итераций неким максимумом. Если точка не вышла за указанную границу, можно считать, что она находится внутри множества.
Точкам около границы множества нужно больше итераций для ухода в бесконечность. Поэтому такие области прорисовываются заметно дольше. Чем дальше от границ множества, тем выше скорость ухода в бесконечность. Для таких точек требуется меньше итераций.
Оптимизация
Одним из способов уменьшения объёма вычислений при вычислении общей картины множества может служить проверка, попадает ли точка в область главной кардиоиды . Формула кардиоиды в полярных координатах выглядит следующим образом:
Таким образом, для точки необходимо вычислить
ρ = (x − 1 4) 2 + y 2 {\displaystyle \rho ={\sqrt {\left(x-{1 \over 4}\right)^{2}+y^{2}}}} , θ = atn 2 (y , x − 1 4) {\displaystyle \theta ={\hbox{atn}}_{2}\left(y,x-{1 \over 4}\right)} , ρ c = 1 2 − 1 2 cos θ {\displaystyle \rho _{c}={1 \over 2}-{1 \over 2}\cos \theta } .Если ρ ≤ ρ c {\displaystyle \rho \leq \rho _{c}} то точка (x , y) {\displaystyle (x,y)} попадает внутрь множества и закрашивается чёрным цветом, а итеративные вычисления можно пропустить.
На практике наибольшее уменьшение объёма вычислений даёт трассировка границы: если есть некоторая замкнутая кривая, не пересекающая ось абсцисс, каждая точка которой уходит за предел bail-out за одинаковое число итераций или, наоборот, принадлежит множеству Мандельброта, то любая точка внутри этой кривой будет обладать тем же свойством, и следовательно вся область внутри границы закрашивается одинаковым цветом.
Связь с множеством Жюлиа
Множество Мандельброта изначально было построено как каталог множеств Жюлиа : каждой точке на комплексной плоскости соответствует своё множество Жюлиа. Точки, принадлежащие множеству Мандельброта, соответствуют связным множествам Жюлиа, а точки не принадлежащие - несвязным .
Отсюда понятно, что интересные варианты множества Жюлиа соответствуют точкам, лежащим на границе множества Мандельброта. Точки глубоко внутри образуют простые геометрические фигуры, а внешние выглядят как пыль, окружающая цветные пятна. Некоторые программы, например, Fractint, позволяют пользователю прямо на экране указать точку, для которой необходимо построить соответствующее множество Жюлиа, упрощая поиск красивых изображений.
Множество Мандельброта и само содержит структуры, напоминающие множество Жюлиа: для любого c {\displaystyle c} область множества Мандельброта около c {\displaystyle c} напоминает центр множества Жюлиа с параметром c {\displaystyle c} . Если сильно увеличить множество Мандельброта в граничной точке c и то же самое проделать с множеством Жюлиа для этого же значения c и в этой же точке, то картины будут асимптотически стремиться друг к другу при всё больших увеличениях.
Вариации множества Мандельброта
Зачастую под названием «Множество Мандельброта» понимается только множество, описанное выше. Однако любая функция комплексной переменной имеет соответствующее множество Мандельброта, которое также характеризуется наличием или отсутствием связного множества Жюлиа. Например, можно положить f c (z )=z 3 +c . Тогда для каждого значения c проверяется связность множества Жюлиа функции f c , и при наличии связности считается, что c принадлежит множеству Мандельброта. В описанном случае связность можно проверить тем же способом, что и для f c (z )=z 2 +c .
Эти утверждения можно обобщить и на множества Жюлиа, определяемые больше, чем двумя числами. Например, множество Жюлиа, определяемое тремя действительными числами, имеет соответствующее трёхмерное множество Мандельброта.
Рассматриваются и многомерные вариации множества Мандельброта. Так, трёхмерный аналог получил название лампочка Мандельброта .
Применение множества Мандельброта в искусстве
Поиск красивых изображений множества Мандельброта - интересное хобби для очень многих людей. Они собирают коллекции таких изображений, причём каждое из них может быть описано небольшим количеством параметров, например, просто координатами центра.

Координаты центра:
-1.7433419053321,
0.0000907687489,
ширина 0.00000000374

Координаты центра:
-1.88488933694469,
8.1387E-10,
ширина 2.4E-13
- Граница между европой и азией Америка относится к европе
- Как экономить деньги при маленькой зарплате?
- Порядок получения жилищной субсидии для военнослужащих
- Лимит кассы: нормативная база и сроки установления лимита
- Полная система вычетов Алгебраическая форма комплексного числа
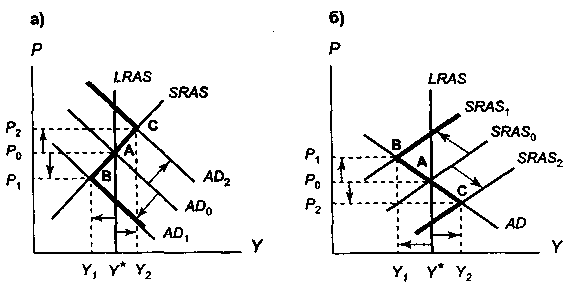
- Модель «Совокупный спрос – совокупное предложение Увеличение совокупного спроса вызывает
- Что называется периодом в физике
- Виды и типы недвижимости, их экономическая составляющая Поля инициализаторов типа
- Экономика, население и города Чеченской Республики
- Особенности проведения региональной программы материнский капитал в московской области Региональный материнский капитал программе семья
- Должностная инструкция страхового агента росгосстрах
- Учет материалов на складе и в бухгалтерии
- На вопрос «Можно ли строить дом без разрешения на строительство?
- Ип на осно какие налоги платит?
- Доходы и расходы будущих периодов Как распределить расходы, затрагивающие несколько налоговых периодов
- Экономические циклы, их особенности и виды
- Необходимо знать от чего зависят цены на жилье
- Контрольная работа: Экономическая мысль Древней Греции
- Бухгалтерские проводки по реализации товаров и услуг 1с бухгалтерия 8
- Оборотные активы организации